Сторона правильного шестиугольника равна 2м. на сколько длина описанной окружности больше длины вписанной окружности?
Ответы
Тк у тебя правильный шестиугольник, то его можно разбить на 6 маленьких правильных треугольников (как торт), где вершина у всех треугольников общая - центр вписанной и описанной окружности (тк правильный 6угольник, то центры совпадают). Радиус описанной будет равен стороне шестиугольника (или треугольника, не важно, тк они правильные), а радиус вписанной будет равен высоте одного такого треугольника. => R=2м r=sgrt3. Сравним: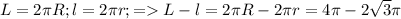 это примерно равно 1.68. Какое-то странное у тебя задание, вот если бы во сколько раз надо было посчитать, то еще нормально, а так не очень.
это примерно равно 1.68. Какое-то странное у тебя задание, вот если бы во сколько раз надо было посчитать, то еще нормально, а так не очень.
ПОКАЗАТЬ ОТВЕТЫ
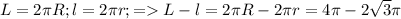 это примерно равно 1.68. Какое-то странное у тебя задание, вот если бы во сколько раз надо было посчитать, то еще нормально, а так не очень.
это примерно равно 1.68. Какое-то странное у тебя задание, вот если бы во сколько раз надо было посчитать, то еще нормально, а так не очень.
Другие вопросы по теме Математика
Популярные вопросы
- Найти точку в координатах хиу на числовой окружности1. М (7п/3)2. М(-16п/3)...
3 - Из двух прямоугольных треугольников ABD и BCD, сумма всех катетов которых равна...
3 - ВОПРОСЫ ПО МУЗЫКЕ НУЖНЫ ОТВЕТЫ...
1 - Найди число,3/5часть которого равна (-1 1/6)...
3 - Биология А, В и С являются необходимыми веществами для роста. Мутантный штамм с...
2 - Как читаются периодические дроби: 0,333... 0,21666... 0,1444... 0,151515... -1,222......
3 - Составить диалог по мультфильм самый большой друг...
2 - Дано- CD-Биссектриса LC Угор ADC равен углу BDC Доказать Треугольник ACD равен...
2 - Молекулярная физика. Решите Дано | СИ ( если требуется) | Решение...
1 - 2. ответьте на вопросы! 1) Wann stehst du auf? 2) Am welchen Wochentagen hast du...
1