1. Математика
  2. сторона, перпендикулярная диагональной

сторона, перпендикулярная диагональной стороне равносторонней трапеции b, образует угол α с большим основанием. найти поверхность тела, образованную вращением вокруг большого основания трапеции​

asylkhanova05 asylkhanova05    2   30.08.2020 21:02    1

Ответы
gona1 gona1  15.10.2020 16:28

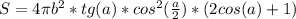
ответ: S=4\pi b^2*tg(a)*cos^2(\frac{a}{2})*(2cos(a)+1)

Пошаговое объяснение:

Опускаем высоты BL и СR, тогда:

AL=RD=bcos(a)\\AD=\frac{b}{cos(a)}\\BC= LR = AD-2AL = \frac{b}{cos(a)} -2bcos(a) = b(\frac{1}{cos(a)} -2cos(a))=\\=b\frac{1-2cos^2(a)}{cos(a)}

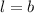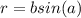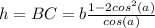При вращении данной трапеции вокруг большего основания получаем два конуса с образующими равными l=b основанием c радиусом r=bsin(a), а также цилиндром с тем же самым радиусом основания и высотой h=BC=b\frac{1-2cos^2(a)}{cos(a)} .

Площадь боковой поверхности конуса: S_{1} =\pi rl

Площадь боковой поверхности цилиндра: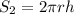 S_{2} =2\pi rh

Тогда площадь боковой поверхности всей фигуры:

S=\pi r (2l +2h)=2\pi bsin(a)(b+b\frac{1-2cos^2(a)}{cos(a)}) = 2\pi b^2\frac{(sin(a))(cos(a)+1-2cos^2(a))}{cos(a)} =\\=2\pi b^2\frac{sin(a)(1-cos(a))(2cos(a)+1)}{cos(a)} =4\pi b^2*tg(a)*cos^2(\frac{a}{2})*(2cos(a)+1)


сторона, перпендикулярная диагональной стороне равносторонней трапеции b, образует угол α с большим
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
1234555676 1234555676  13.06.2019 07:10
Запишите три десятичные дроби, равные числу 5,070...
Вася2288221 Вася2288221  13.06.2019 07:10
Найдите квадрат и куб числа: а)25 б)30 в)50 г)100...
KIMSEOLHYUN KIMSEOLHYUN  13.06.2019 07:10
Вшкольном саду на клумбах посадили 900 цветов причем 630 из них тюльпаны а остальные розы на клумбах с тюльп. посадили 35 цв. на каждую клумбу а на клумбе с розами 30 цв. сколько...
канна канна  13.06.2019 07:10
Уменя примеры по действиям : 7,500+72 - 250*2= 160: 80*100+12,000 - 2,000= (108 - 108: 4): 3*10,000= 15+360,000: 100 - 3,000=...
Farzaney Farzaney  13.06.2019 07:10
Дроби к наименьшему общему знаменателю: a)3/5 и 4/7 б)2/5 и 5/18 в)5/14 и 8/35...
leraklybnika leraklybnika  13.06.2019 07:10
На сколько наименьшее четырехзначное число меньше наибольшего четырехзначного числа...
Sashunya20061 Sashunya20061  13.06.2019 07:10
Найдите наименьшее составное натуральное число, которое не делится ни на одно из натуральных чисел от двух от десяти....
ЕленаФроленкова ЕленаФроленкова  13.06.2019 07:10
)ученик выполнил деление 148: 15=8 (остаток 28 ) в чём заключается ошибка? выполни деление правильно....
км2002 км2002  13.06.2019 07:10
Выразите: а)3,8 см в сантиметрах и миллиметрах б)4,05 кг в килограммах и граммах...
AmoskovaAlenka AmoskovaAlenka  13.06.2019 07:10
Распредилительный закон вычислите с арифметических законов 560*188-880*56...

Популярные вопросы