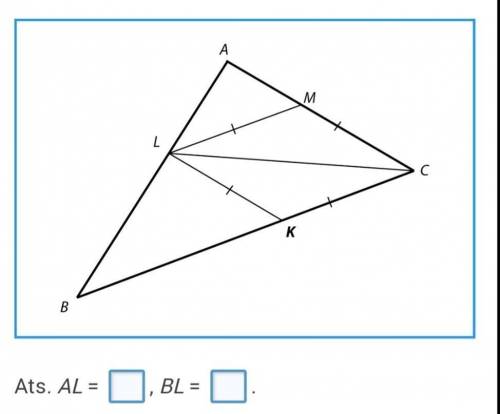
Сторона AB=12 см, BC=14 см, AC=10 см
найти AL, BL

AL = 5 см; BL = 7 см

Пошаговое объяснение:

Дано: ΔАВС.

LM = MC = CK = LK;

AB = 12 см, BC = 14 см,  AC = 10 см.

Найти: AL; BL.

Решение.

1. Рассмотрим LMCK.

Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник - параллелограмм.

⇒ LM || BC; LK || AC.

2. Рассмотрим ΔLAM и ΔABC.

Пусть LM = MC = CK = LK = а

LM || BC (KLMC - параллелограмм)

Лемма. Если две стороны треугольника пересекает прямая, параллельная третьей стороне, то она отсекает треугольник, подобный данному.

⇒  ΔLAM ~ ΔABC.

Составим отношение сходственных сторон:

3. Рассмотрим ΔBLK и ΔABC.

LK || AC (KLMC - параллелограмм)

⇒ ΔBLK ~ ΔABC.

Составим отношение сходственных сторон:

4. Найдем отношение AL и BL:

Пусть AL = 5x; тогда BL = 7x

Составим уравнение:

5х + 7х = 12

12х = 12

х = 1

⇒ AL = 5x = 5 (см);  BL = 7x = 7 (см)