Сточными науками горе-гуму : ( выбрали произвольное целочисленное решение неравенства 48 - 13х - х² ≥ 0. какова вероятность того, что выбранное число будет также и решением неравенства: а) х²> 0 б)х² + 10х ≤ 0 в) х² < 101 г) 4х² - 20х + 21 < 0?
Другие вопросы по теме Математика
Популярные вопросы
- Эссе на тему: Можно ли существовать без системы социального обеспечения?...
1 - Определи массовую долю (в %) серы в технической сере, если при сжигании 8,06 г технической...
1 - Особливістю 1990-х рр. стало швидке зростання експорту з нових індустріальних країн...
3 - Истории как я сходил в цирк...
2 - решить элементарное задание , которое завело в тупик...
3 - Хромосомный набор карликового шимпанзе содержит 48 хромосом. Это критерий: морфологический...
1 - Найдите в таблице примеры с равными ответами. 99-9 56-6...
1 - Дана правильная четырехугольная усечённая пирамида ABCDA1B1C1D1. Стороны ее оснований...
2 - Определите химические элементы по распределению электронов в его атоме : 2, 3; 2е-,8е-,3е-...
2 - ответить, до 13, на 9 не нужно ...
1
Решением неравенства 48 - 13х - х² ≥ 0 есть множество чисел [-16;3] , в котором содержится 20 целых чисел.
а) из этих двадцати чисел только 3 удовлетворяют неравенству х²>0 (1, 2 и 3), значит вероятность будет равна 3/20
б) решением неравенства х² + 10х ≤ 0 есть множество чисел [-10;0] , в котором содержится 11 целых чисел. Все они попадают во множество [-16;3] . Вероятность равна 11/20
в) решением неравенства х² < 101 есть множество чисел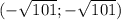 , в котором содержится 21 целое число, из которых 14 попадают во множество [-16;3] (числа от -10 до 3) . Вероятность равна 14/20 = 7/10
, в котором содержится 21 целое число, из которых 14 попадают во множество [-16;3] (числа от -10 до 3) . Вероятность равна 14/20 = 7/10
г) решением неравенства 4х² - 20х + 21 < 0 есть множество чисел (1,5; 3,5) , в котором содержится 2 целых числа (2 и3), оба попадают во множество [-16;3]. Вероятность равна 2/20 = 1/10