Срешением. используя формулу ньютона- лейбница, вычислите определенный интеграл:
Другие вопросы по теме Математика
Популярные вопросы
- Составить по тему моя будущая проффесия...
3 - Вычислите значение выражений наиболее удобным по действиям ) 1)0,42*5,19+5,19*0,58...
3 - Разобраться! определите падеж имен существительных: сварил кофейку !...
2 - Смесь ортофосфата кальция, кокса и песка нагревали в электрической печи. один...
1 - Надо слова мужского и женского рода с окончанием ь после шипящих...
2 - Переведите на язык the more i learn english, the letter i can speak it....
2 - Дана арифметическая прогрессия. вычислите а6 если а4=-16 д=-2...
3 - Вкаком из предложений пропущена одна (только одна! ) запятая? - работа не выполнена!...
3 - Тема: средняя линия треугольника. в δавс точки м , n и к - середины сторон...
3 - Рассчитайте массу выпавших кристаллов нитрата калия,если 100 г насыщенного...
3
1)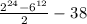
2)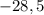
3)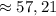
Пошаговое объяснение: