Срешением, хотя бы только первого доказательства

а) доказать, то AD || BC:

Угол EAB - развёрнутый. Значит ∠EAC = 180°-∠BAC. Так как AD - биссектриса угла EAC, то ∠DAC = ∠DAE = 1/2∠EAC = (180°-∠BAC):2.

Рассмотрим треугольник ABC. Он равнобедренный, т.к. AB = BC. Тогда

∠ABC = ∠ACB = (180°-∠BAC):2

Получается, что ∠ACB = ∠DAC. Эти углы - накрест лежащие. Значит AD || BC.

ч.т.д.

б) найти :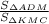

Так как AD || BC, углы ADM=CKM и DAM=KCM как накрест лежащие.

По первому признаку подобия треугольники ADM и KMC подобны. По условию AM/MC = 5/3 - коэффициент подобия.

Отношение площадей подобных треугольников равно квадрату коэффициента подобия, то есть .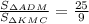

в)