Срешение, )) найти все значения параметра а, при каждом из которых уравнение ах^2+(4а-7)х+4а-5=0 имеет в точности один корень на отрезке [-4; 0].

Ответы

Denis1930 09.10.2020 06:09

Рассмотрим функцию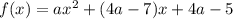 f(x) = ax^2+(4a-7)x+4a-5 .

1. Если a = 0, то f(x) - прямая линия (имеет ровно одно пересечение с Ox). Проверим, входит ли он в промежуток: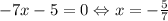 $-7x-5 = 0 \Leftrightarrow x = -\frac{5}{7}$ - подходит.

2. a > 0. Если абсцисса вершины параболы неотрицательна ( $x_{0}\geq 0\Leftrightarrow\frac{7-4a}{2a}\geq 0\Leftrightarrow a\in(0; \frac{7}{4}]$ ), то

$\left \{ {{f(0)}\leq 0\atop {f(-4)}\geq 0} \right. \left \{ {{4a-5\leq 0} \atop {4a+23\geq0} } \right. \left \{ {{a\leq\frac{5}{4}} \atop {a\in[-\frac{23}{4}; +\infty)}} \right. \Rightarrow a\in (0; \frac{5}{4}]$

Если $x_{0}\leq -4\Leftrightarrow\frac{7-4a}{2a}\leq -4\Leftrightarrow\frac{7+4a}{2a}\leq 0\Leftrightarrow a\in[-\frac{7}{4}; 0)$ , то ветви параболы будут направлены вниз, что не подходит для данного случая.

Если $-4\leq x_{0}\leq 0 \Rightarrow \left \{ {{a\in(-\infty; 0)\cup[\frac{7}{4}; +\infty)} \atop {a\in(-\infty; -\frac{7}{4}]\cup(0; +\infty)}} \right. \Rightarrow a\in[\frac{7}{4}; +\infty)$

$\left \{ {{f(0)}\leq 0\atop {f(-4)}\geq 0} \right. \Rightarrow a\in (0; \frac{5}{4}] \Rightarrow a\in\varnothing\\ \left \{ {{f(0)}\geq0 \atop {f(-4)}\leq0} \right. \left \{ {{a\leq -\frac{23}{4}} \atop {a\geq \frac{5}{4}}} \right. \Rightarrow a\in\varnothing$

3. a < 0. Если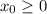 $x_{0}\geq 0$ , то ветви направлены вверх.

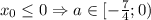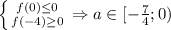
Если $x_{0}\leq 0 \Rightarrow a\in[-\frac{7}{4}; 0)$ , то $\left \{ {{f(0)}\leq 0 \atop {f(-4)}\geq 0} \right. \Rightarrow a\in[-\frac{7}{4}; 0)$

Если $-4\leq x_{0}\leq 0 \Rightarrow a\in(-\infty; -\frac{7}{4}]$ , то

$\left \{ {{f(0)}\leq 0 \atop {f(-4)} 0} \right. \Rightarrow a\in(-\frac{23}{4}; -\frac{7}{4}]\\ \left \{ {{f(0)}\geq 0 \atop {f(-4)}\leq 0} \right. \Rightarrow a\in\varnothing$