Спростити вираз:
а) cos²a+1/1+ctg²a-1
б) sin(p/2+a)+cos(p-a)-tg(3p/2-a)
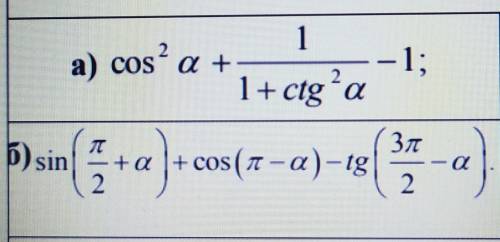
Другие вопросы по теме Математика
Популярные вопросы
- Автомашина на 1 км пути расходует в среднем 200 г бензина сколько бензина израсходовал...
3 - Продолжить предложение _золоті бані софійського собору видні...
2 - Задайте все виды вопросов i go to school by 8: 30....
1 - Как изменится погода, если ветер дует из пустыни - ветер дует из океана...
3 - Диагональ ромба образует с одной из ее сторон угол 40°. найдите все углы ромба....
3 - Сраствором перманганата калия реагируета а) пропан б) пропен в) бензол г) бутан...
2 - 1.определите количество соляной кислоты массой 710г. 2.при взаимодействии цинка...
2 - Найдите в каждой группе предложений многозначные слова.обьясните их значения.расцвёл...
1 - Решите в целых числах уравнение 2m^2 - 2mn+9m+n= 2...
2 - Контрольний твір-роздум за твором панаса мирного чи нечуя левицького)...
3
а) Для упрощения выражения cos²a+1/1+ctg²a-1, мы можем использовать тригонометрические тождества. Воспользуемся формулой "Разложение суммы квадратов":
cos²(a) = (cos(a))²
ctg²(a) = 1/(tan(a))² = (cos(a)/sin(a))² = (cos²(a))/(sin²(a))
Теперь мы можем переписать наше исходное выражение следующим образом:
cos²a+1/1+ctg²a-1 = (cos(a))² + 1/(1+(cos²(a))/(sin²(a))) - 1
Заметим, что 1+(cos²(a))/(sin²(a)) = (sin²(a)+cos²(a))/(sin²(a)) = 1/(sin²(a))
Теперь мы можем продолжить упрощение:
(cos(a))² + 1/(1+(cos²(a))/(sin²(a))) - 1 = (cos(a))² + sin²(a)/(sin²(a)) - 1
= (cos(a))² + 1 - 1
= (cos(a))²
Таким образом, исходное выражение упрощается до (cos(a))².
б) Для упрощения выражения sin(p/2+a)+cos(p-a)-tg(3p/2-a), мы также можем использовать тригонометрические тождества.
Давайте разберем каждое слагаемое по отдельности:
sin(p/2+a):
Мы знаем, что sin(p/2+a) = cos(a), согласно тригонометрическому тождеству sin(x+y) = cos(x).
cos(p-a):
Также, мы знаем, что cos(p-a) = cos(-a) = cos(a), согласно свойствам косинуса.
tg(3p/2-a):
Рассмотрим tg(3p/2-a). Используем формулу касательной слагаемых:
tg(3p/2-a) = sin(3p/2-a)/cos(3p/2-a)
Заметим, что sin(3p/2-a) = sin(p/2+a) и cos(3p/2-a) = cos(p-a), поэтому мы можем заменить их на ранее упрощенные значения:
tg(3p/2-a) = sin(p/2+a)/cos(p-a) = cos(a)/cos(a) = 1
Теперь, когда мы упростили каждое слагаемое, мы можем записать их сумму:
sin(p/2+a)+cos(p-a)-tg(3p/2-a) = cos(a) + cos(a) - 1
= 2cos(a) - 1
Таким образом, исходное выражение упрощается до 2cos(a) - 1.
Надеюсь, это помогает! Если у вас есть дополнительные вопросы, не стесняйтесь задавать их.