Сподробным обьяснением решить .
сережа задумал два натуральных числа.он забыл задуманные числа,но точно помнит,что их сумма равна 22,а про разность абсолютно уверен,что она меньше 14,но больше 10.какие два числа задумал сережа? найдите все варианты и докажите,что других нет.

Ответы

Glenchittt1 18.09.2020 01:19

Единственно возможный вариант - 17, 5.

Пошаговое объяснение:

Обозначим числа как и .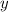

Если сумма двух чисел - чётное число, то чётность искомых чисел одинакова, то есть или оба числа чётные или оба нечётные.

Но если числа одинаковой чётности, то разность будет тоже чётной. Между 10 и 14 только 1 чётное число - это 12, так как мы не считаем 10 и 14.

Теперь составляем систему уравнений:

$\left \{ {{x+y=22} \atop {x-y=12}} \right.$

Сложим уравнения:

(x+y)+(x-y)=22+12

Упростим правую часть:

(x+y)+(x-y)=34

Упростим левую часть:

2x+y-y=34

И ещё раз её упростим:

2x=34

Теперь легко найти :

$x=34:2\\x=17$

Находим :

$y=22-17\\y=5$

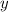Вывод: Единственный возможный вариант - 17, 5.

УДАЧИ! ОБРАЩАЙТЕСЬ!

ПОКАЗАТЬ ОТВЕТЫ

28916587 18.09.2020 01:19

ответ: 5 и 17.

Обозначим искомые числа за x и y. Тогда: x + y = 22.

Если сумма двух чисел - это четное число, то оба числа были одной и той же четности (то есть либо оба нечетные, либо оба четные).

Но и разность чисел одной четности - это тоже четное число. Поэтому x - y - это обязательно четное число. Но среди чисел меньше 14 и больше 10 только одно четное число, это 12 (считаем, что разность не может быть равна 10 и 14).

Тогда мы можем составить и решить эту систему уравнений:

$\left \{ {{x + y=22} \atop {x - y=12}} \right.$