1. Математика
  2. Сответом: доказать, что векторы

Сответом: доказать, что векторы а, b, с образуют базис, и найти координаты вектора d в этом базисе: а=(11,1,2), b=(-3,3,4), с=(-4,-2,7), d=(-5,11,-15). )

Electron57 Electron57    2   13.08.2019 11:32    0

Ответы
28ByaKa28 28ByaKa28  04.10.2020 15:51

Вычислим определитель матрицы перехода, составленной из координат векторов

\displaystyle\left|\begin{array}{ccc}11&1&2\\ -3&3&4\\-4&-2&7\end{array}\right|= 11\cdot 3\cdot 7+1\cdot 4\cdot(-4)+(-3)\cdot (-2)\cdot 2-\\ \\ \\ -(2\cdot 3\cdot (-4)+(-2)\cdot 4\cdot 11+ 7\cdot 1\cdot (-3))= 360\ne 0

Так как определитель матрицы перехода не равен нулю, то ранг этой матрицы равен трем и из теоремы о базисном миноре следует, что векторы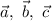 \vec{a},~\vec{b},~\vec{c} линейно независимы и могут быть приняты в качестве базиса пространства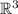 \mathbb{R}^3

Соотношение, записанное для векторов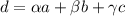 d=\alpha a+\beta b+\gamma c, справедливо для каждой из проекций:

\begin{cases}&\text{}\alpha\cdot 11+\beta \cdot 1+\gamma\cdot 2=-5\\&\text{}\alpha \cdot (-3)+\beta \cdot 3+\gamma \cdot 4=11\\&\text{}\alpha\cdot(-4)+\beta\cdot(-2)+\gamma\cdot 7=-15\end{cases}~~\Rightarrow~~\begin{cases}&\text{}\alpha =-\dfrac{59}{90}\\&\text{}\beta=\dfrac{83}{18}\\&\text{}\gamma=-\dfrac{6}{5}\end{cases}

вектор d имеет разложение в базисе a, b, c:

\vec{d}=-\dfrac{59}{90}\vec{a}+\dfrac{83}{18}\vec{b}-\dfrac{6}{5}\vec{c}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
tawawma tawawma  04.08.2019 18:00
Равносильно ли уравнения -х^3-2х^2-3х-6=0 и х^3+2х^2-3х+6=0...
  04.08.2019 18:00
Два велосипедиста едут по окружности, начав одновременно двигаться из одного места. скорость первого — 36 км/ч, второго — 30 км/ч. когда первый велосипедист проехал...
светлана440 светлана440  04.08.2019 18:00
Обьясните кто-нибудь как это решается у нас тема подобных слагаемых, как их вообще приводить? вот пример - 5m - (3m + 5) + (2m - 4) , напишите как решать, ответ не...
Zarinaoo Zarinaoo  04.08.2019 18:00
7метров что больше 9 дециметров что больше...
sevaismailova2 sevaismailova2  04.08.2019 18:00
Решить : в одном городе начинаются три туристических теплоходных рейса. первый длиться 12 суток, 2-ой 18 суток, а 3-ий 21 сутки. сегодня из города вышли теплоходы по...
NerminJaleÇiçek NerminJaleÇiçek  04.08.2019 18:00
Почему леонарда да винчи делал иллюстрации к трактатам ветрувия? почему новое произведение искусства не отрицает старые, как это происходит в науке...
annareain252 annareain252  04.08.2019 18:00
1. определите, какие из следующих предложений являются высказываниями, а какие нет: а) для каждого из нас учить второй иностранный язык легче, чем первый. б) какой...
yakovlevakristi yakovlevakristi  04.08.2019 18:00
Как записать решение у аси 36р., а у вити 59р. сколько часов они смогут купить, если одни часы стоят 45р.?...
zaika25901 zaika25901  04.08.2019 18:00
Из 18 одинаковых кубиков сложили прямоугольный параллелепипед высотой 3 кубика.найдите площадь параллелепипеда ,если площадь поверхности одного кубика равна 6 кв.см....
dnlnv dnlnv  04.08.2019 18:00
Тендеу куру аркылы шыгару. биринши суйыккоймадагы мунай екиншидегисине караганда 3 есе артык. егер екинши суйыккоймадагы мунай 216 т артык болса, онда арбир суйыккоймада...

Популярные вопросы