Составьте уравнение прямой, проходящей через точку A(2;-3) и имеющей направляющий вектор n {4;-1}.
Другие вопросы по теме Математика
Популярные вопросы
- Расположите в порядке возрастания числа -6; 5,3; 0,5; -5,9; 0; -11; 4,5...
2 - Твір мініатюра 7-8 речень на тему чи потрібні друковані книги (20 )...
3 - Полировочная машина за 2 ч. работы израсходовала 36 л бензина.сколько часов...
1 - Решить . два спортсмена начали бег одновременно навстречу друг другу с...
2 - Найди значения выражения по образцу: 3m 7cm - 25cm + 4m 18cm=7m 1)307-25=...
1 - Wie gut kennst du berlin? 1.ordne die informationen einander zu und fülle...
3 - Написать ! как написать уравнение реакции, если золото превращается в золото...
2 - Образуйте и запишите новые слова с приставками за-, пере-, писать, бежать,...
2 - Решить : 1)какая масса фосфорной кислоты вступит в реакцию с оксидом калия...
3 - Решите уравнение. 2/7(y-7)-3/4(y-8)=17...
1
(x-2)/4 = (y+3)/-1 — каноническое
x+4y+10 = 0 — общее
Пошаговое объяснение:
Зная направляющий вектор прямой и точку, через которую она проходит, можно записать каноническое уравнение прямой. Оно имеет вид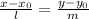 , где (x_0; y_0) — координаты точки на прямой, (l; m) — направляющего вектора. Подставим числа из условия и получим
, где (x_0; y_0) — координаты точки на прямой, (l; m) — направляющего вектора. Подставим числа из условия и получим
Если требуется, преобразуем к общему: