1. Математика
  2. составить уравнение плоскости

составить уравнение плоскости которая проходит через две точки: A (1;-2;-8) B(4;5;2) перпендикулярно к плоскости x-2y+3z-5=0

dzubanuksofia dzubanuksofia    1   25.11.2020 12:40    1

Ответы
ДашаНифонтова ДашаНифонтова  25.12.2020 12:41

\sigma _2 : 41x+y-13z-145=0

Пошаговое объяснение:

1) Найдем вектор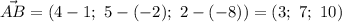 \vec{AB} = (4-1;\ 5-(-2);\ 2-(-8)) = (3;\ 7;\ 10)

2) Из уравнения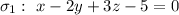 \sigma _1:\ x-2y+3z-5=0 снимем вектор нормали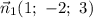\vec{n}_1(1;\ -2;\ 3)

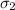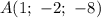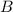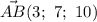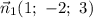3)Уравнение плоскости \sigma_2 составим по точке A(1;\ -2;\ -8) (Можно взять и B) и двум неколлинеарным векторам \vec{AB}(3;\ 7;\ 10) и \vec{n}_1(1;\ -2;\ 3):

\left[\begin{array}{ccc}x-1&3&1\\y+2&7&-2\\z+8&10&3\end{array}\right] = 0\\\\\\(x-1)\left[\begin{array}{cc}7&-2\\10&3\end{array}\right] - (y+2)\left[\begin{array}{cc}3&1\\10&3\end{array}\right] + (z+8)\left[\begin{array}{cc}3&1\\7&-2\end{array}\right] =0\\\\\\(x-1)(21+20) - (y+2)(9-10)+(z+8)(-6-7)=0\\\\41(x-1)+(y+2)-13(z+8)=0\\\\41x-41+y+2-13z-104 = 0\\\\\sigma _2 : 41x+y-13z-145=0

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
panda4918 panda4918  27.04.2020 17:28
Hello my friends plis help my...
AbraevAidar AbraevAidar  27.04.2020 17:28
Округлити: 1 до сотень: а).45245; б).91897 2 до десятків тисяч: а).159752; б).523541 3 до сотень тисяч: а).523541; б).975397...
Masha36127 Masha36127  27.04.2020 17:28
Могут ли расстояние от некоторой точки на плоскости до вершин квадрата со стороной , где − натуральное, быть равным 1, 5, 8 и 9?...
Kseiaa Kseiaa  27.04.2020 17:28
Найдите наименьшее целое число , удовлетворяющее неравенству 1. у-1/5-у у/5 ответ: 2. 2у-4/3-у+1/5 1 ответ...
Guletta Guletta  27.04.2020 17:28
Відстань від центра кола до прямої дорівнює 7 см, а радіус кола 5 см. Як розміщені пряма і коло?​...
лимон2509 лимон2509  27.04.2020 17:28
с математикой упр 147 (а, б, в)...
Alexandra335 Alexandra335  27.04.2020 17:28
1. Якщо висота піраміди проектується в центр описаного навколо основи кола, то: А). Всі бічні ребра рівні; Б). Всі висоти бічних граней рівні; В). Всі двогранні кути при основі...
1trippy1 1trippy1  27.04.2020 17:28
Вычислите а)Нод (816;51) б)Нок (24;25)​...
Лера15012003 Лера15012003  27.04.2020 17:28
Две семьи отправились на детский утренник. Первая семья купила два детских билета и один взрослый и всего заплатила 350 рублей. Вторая семья купила три детских билета и два взрослых...
айрин429 айрин429  27.04.2020 17:28
Запишите формулы прямой пропорциональности,3) у = -3x;(7) y = 15x;1)-12;4) y = 0,8x;6) у = - 2x;8)=x+3Можете черчение прямой пропорционалности именно а не ответы​...

Популярные вопросы