Составить уравнение касательных к гиперболе 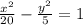перпендикулярных прямой 4x+3y-7=0

Для составления уравнения касательной к гиперболе, перпендикулярной данной прямой, нам необходимо сначала найти точку касания на гиперболе. Затем мы воспользуемся свойствами производной, чтобы найти угловой коэффициент касательной, и, наконец, составим уравнение касательной.

1. Найдем точку касания. Для этого решим систему уравнений, состоящую из гиперболы и прямой:
...(1)
4x + 3y - 7 = 0 ...(2)

В системе уравнений, приведенной выше, у нас есть два уравнения и две неизвестные (x и y). Мы можем решить систему двумя способами: методом подстановки или методом сложения/вычитания.

Пусть мы воспользуемся методом сложения/вычитания:

Умножим уравнение (2) на 5, чтобы коэффициент при y стал таким же, как в уравнении гиперболы:

20x + 15y - 35 = 0 ...(3)

Теперь сложим (1) и (3):


20x + 15y - 35 = 0

Уберем дробь в уравнении гиперболы:

x^2 - 4y^2/5 = 20 ...(4)

Теперь сложим (3) и (4) почленно:

20x + x^2 - 4y^2/5 + 15y - 35 = 20

Перепишем уравнение в стандартной форме:

x^2 + 20x - 4y^2/5 + 15y = 55 ...(5)

Раскроем квадратное слагаемое x^2 + 20x, дополнив его слагаемыми и исключив их же:

(x^2 + 20x + 100) - 100 - 4y^2/5 + 15y = 55

(x + 10)^2 - 100 - 4y^2/5 + 15y = 55

(x + 10)^2 - 4y^2/5 + 15y - 155 = 0 ...(6)

Получили уравнение гиперболы после сложения с (3) - полученного уравнения, перпендикулярного прямой 4x+3y-7=0.

Теперь мы можем найти точку касания путем решения системы уравнений (5) и (6):

x^2/20 - y^2/5 = 1 ...(7)
(x + 10)^2 - 4y^2/5 + 15y - 155 = 0 ...(6)

Решая данную систему уравнений, мы найдем x и y координаты точки касания гиперболы и прямой.

2. Теперь нам нужно использовать свойства производной, чтобы найти угловой коэффициент касательной. Воспользуемся уравнением гиперболы и продифференцируем его по x.

d/dx (x^2/20 - y^2/5) = d/dx (1)

2x/20 - (2y)(dy/dx)/5 = 0
x/10 - y(dy/dx)/5 = 0
dy/dx = (5x)/(10y)

Мы нашли угловой коэффициент касательной к гиперболе в точке касания.

3. Итак, мы знаем точку касания (x, y) и угловой коэффициент касательной. Мы можем использовать эти данные, чтобы составить уравнение касательной в точке (x, y):

Используем формулу точки-наклона для уравнения прямой:

y - y_1 = m(x - x_1)

Подставим координаты точки касания (x, y) и угловой коэффициент m в уравнение:

y - y_1 = (5x)/(10y)(x - x_1)

Итак, мы составили уравнение касательной к гиперболе, перпендикулярной прямой 4x+3y-7=0, в точке (x, y).