составить уравнение касательной к графику функции f(x)=x^2-x^3 проходящей через точку графика с абцисой x0=-1

Ответы

Лара505 05.06.2021 06:00

y(x)=-5x-3

Пошаговое объяснение:

Уравнение касательной к функции f(x) в точке x₀

$y(x)=f'(x_0)\cdot(x-x_0)+f(x_0)$

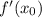где f'(x_0) - значение производной функции f(x) в точке x₀ .

Для данной задачи

$f'(x)=(x^2-x^3)'=2x-3x^2f'(-1)=2\cdot(-1)-3\cdot(-1)^2=-2-3=-5f(-1)=(-1)^2-(-1)^3=1-(-1)=2$

Тогда

$y(x)=-5\cdot(x-(-1))+2$

После раскрытия скобок и приведения подобных

y(x)=-5x-3

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

123451529 26.10.2020 22:26

dasha190800 26.10.2020 22:26

amadi888 26.10.2020 22:26

Я знаю есть кто-то кто решит...

Ronni05 26.10.2020 22:26

Решите интеграл x^2-9/x^2-8 dx...

Lunatuk 26.10.2020 22:26

3/8*(0.64-4.8y)+0.4=5/17*(0.34-5.1y)...

lalal2345 26.10.2020 22:27

nigar26 26.10.2020 22:27

решить линейное уравнение с метода Гаусса,...

loveinyourhard 26.10.2020 22:27

tipikina2016 26.10.2020 22:27

PoliShka18 26.10.2020 22:27

новерное 29 в 9 степени сколько будет...

составить уравнение касательной к графику функции f(x)=x^2-x^3 проходящей через точку графика с абцисой x0=-1​