Составить уравнение касательной к графику 1/х в точке х0=1

Для начала вычислим производную функции:

ее значение производной в точке x0=1 равно

Значение функции в точке x0=1: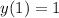

Искомое уравнение касательной:

1. Уравнение касательной к графику функции у=f(х) в точке с абсциссой x₀ имеет вид

у=y( x₀)+f'( x₀)*(x- x₀), где  f'( x₀)- значение производной в точке  x₀,

y( x₀) значение функции в точке  x₀.

2. y( x₀)=у(1)=1/1=1

3. f'( x)=-1/х²

4. f'( x₀)=f'( 1)=-1/1²=-1

5. Искомое уравнение у=1-1*(х-1); у=-х+2

ответ. у=-х+2