Составить уравнение гиперболы, симметричной относительно осей координат, если она проходит через точки М1 (х1, у1) и М2 (х2, у2)
(таблица 3). Найти: 1) действительную и мнимую полуоси;
2) эксцентриситет. Построить гиперболу.
x1=1
x2=3
y1=2
y2=7
Другие вопросы по теме Математика
Популярные вопросы
- Как устранить возможность выпадения синхронного двигателя из...
2 - Записать 10 прилагательных, образовать полную и краткую форму,...
2 - Через точку (pi/2;-1) какой проходит график функции? y=sin y=cos...
2 - Обчисліть об’єм вуглекислого газу (н.у.), який виділиться внаслідок...
1 - решить!Исследование функции и построение её графика...
2 - 3.Выполните синтаксический разбор сс: бл_стят росой, низко расст_лается,...
3 - До ть,будь ласка. Який об єм водню(н.у) виділиться унаслідок...
3 - Вектор передачі COVID-19 знаходиться між 1,5-2, що приблизно...
2 - О каком веществе идет речь: «Белый жирный на ощупь полимер, нерастворим...
1 - О, на вашу думку, спонукає розважливого й практичного Санчо Пансу...
3
Даны точки М1 (1; 2) и М2 (3; 7).
Подставим эти координаты в уравнение гиперболы.
Получаем уравнение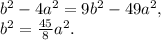
Замена: подставим значение b^2 в первое уравнение.
(1/a^2) -(4/(45/8)a^2) = 1.
Отсюда находим a^2 = 13/45, а b^2 = (45/8)*(13/45) = 13/8.
ответ: уравнение гиперболы (x^2/(13/45)) - (y^2/(13/8)) = 1.
Параметры гиперболы и график приведены во вложении.