Составить канонические уравнения: а) эллипса; б)гиперболы; в) параболы. где а, в - точки, лежащие на кривой, f - фокус, a - большая (действительная) полуось, b - малая (мнимая) полуось, е - эксцентриситет, у = + -kx - уравнения асимптот гиперболы, d - директриса кривой, 2с -фокусное расстояние. a) 2a=22, е= √57/11 ; b) k=2/3; 2c=10 √13 ; c) ось симметрии ox и а(27; 9).
Другие вопросы по теме Математика
Популярные вопросы
- определите электроемкость конденсатора энергия электростатического поля которого...
1 - Назовите наиболее подходящий материал для изготовления игрушек и кукол. -Перечислите...
1 - 2. Замените, где возможно, полную форму прилагательного краткой и запишите. Образец:...
2 - Почему амплитуда достигает максимального значения при совподении с частотой...
1 - Кластерды толыктырыныз : болашақтын мамандыктары...
1 - Вставьте в слова пропущенные буквы. И или Ы....
3 - Задача человек вылетел со скоростью 60 км с другой стороны вылетела подушка вопрос...
2 - Гироскопический датчик Изучи предложенный программный код и определи направление...
3 - Unscramble the words and type them. )mtssarolyessS...
3 - Гарыш Жане Галамтор туралы Макал Мател...
1
a) Эллипс.
2a = 22; a = 11;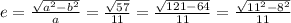 ; b = 8
; b = 8
Уравнение: x^2/a^2 + y^2/b^2 = 1;
x^2/121 + y^2/64 = 1
b) Гипербола.
k = b/a = 2/3; a = 1,5b; 2c = 10√13;
b^2 = 325/3,25 = 100; b = 10; a = 1,5b = 15
Уравнение: x^2/a^2 - y^2/b^2 = 1
x^2/225 - y^2/100 = 1
c) Парабола.
Ось симметрии Ox, на кривой лежит точка A(27; 9)
Уравнение: y^2 = 2px
9^2 = 2p*27
p = 81/(2*27) = (3*27)/(2*27) = 3/2 = 1,5
Уравнение: y^2 = 3x