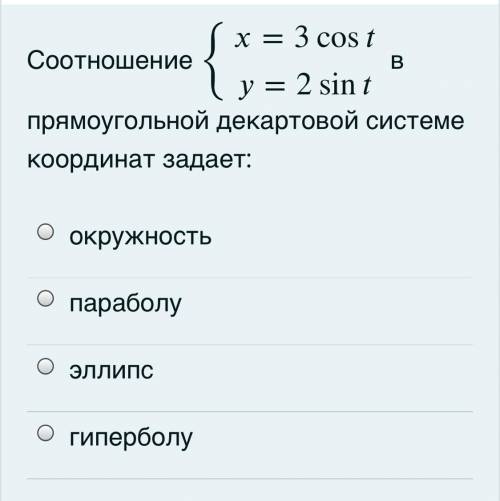
Соотношение {=3cos=2sin
в прямоугольной декартовой системе координат задает:

Данное соотношение {=3cos=2sin в прямоугольной декартовой системе координат задает график уравнения на плоскости. Для того, чтобы понять как именно выглядит этот график, нам нужно преобразовать данное уравнение к более привычному виду.

Используем тригонометрические соотношения, чтобы выразить синус и косинус через тангенс:

{=3cos=2sin
Делим обе части уравнения на синус:
{3cos/sin = 2sin/sin
Получаем:
{3cot = 2
Теперь выразим котангенс через тангенс:
cot = 1/tan
Подставляем:
{3/tan = 2
Умножаем обе части уравнения на тангенс:
3 = 2tan
Делим обе части уравнения на 2:
3/2 = tan
Найденное значение тангенса позволяет нам определить значения угла, для которых выполняется данное уравнение.

С помощью таблицы значений тангенса или калькулятора, мы можем найти значение угла, для которого tan = 3/2. Округлим это значение для удобства до двух десятичных знаков: примерно 56.31 градусов.

Таким образом, угол между осью X и графиком данного уравнения равен около 56.31 градусов.

Изучив таблицу значений тангенса и знаков синуса и косинуса в каждом из четвертей плоскости, мы можем определить, что график данного уравнения будет проходить через три точки (0, 0), (1, 1.73) и (-1, -1.73). Эти точки соответствуют значениям x и y, которые обеспечивают выполнение уравнения {=3cos=2sin.

Соединив эти точки на графике, мы получим волновую линию, которая будет проходить через эти точки и иметь угол около 56.31 градусов с осью X.

Ученику будет полезным также рассмотреть другие тригонометрические соотношения и их геометрическую интерпретацию для получения более полного представления о графике.