События a, b и c независимы; p(a) = 0,7, p(b) = 0,6 и p(c) = 0,3. найдите вероятность события a при усло- вии, что наступило событие a+b+c.

Ответы

karuna4 31.08.2020 09:55

Вероятность события А + В + С:

$P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+\\ \\ +P(ABC)=0.7+0.6+0.3-0.7\cdot 0.6-0.7\cdot0.3-0.6\cdot 0.3+\\ \\ +0.7\cdot 0.6\cdot 0.3=0.916$

Условная вероятность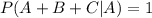 P(A+B+C|A)=1 , тогда по формуле Байеса, искомая вероятность:

$P(A|A+B+C)=\dfrac{P(A+B+C|A)\cdot P(A)}{P(A+B+C)}=\dfrac{1\cdot 0.7}{0.916}=\dfrac{175}{229}\approx0.7642$

Можно еще проще, через вероятность противоположного события,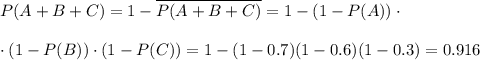 $P(A+B+C)=1-\overline{P(A+B+C)}=1-(1-P(A))\cdot \\ \\ \cdot (1-P(B))\cdot (1-P(C))=1-(1-0.7)(1-0.6)(1-0.3)=0.916$

искомая вероятность аналогично по Байесу.

ПОКАЗАТЬ ОТВЕТЫ

НикитаТим 31.08.2020 09:55

ответ и решение во вложении

События a, b и c независимы; p(a) = 0,7, p(b) = 0,6 и p(c) = 0,3. найдите вероятность события a при

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

Katre678556 29.11.2020 19:04

Обчисліть визначенні інтеграли...

ТАААААААААААПКИ 29.11.2020 19:04

напишите на листке (;´༎ຶٹ༎ຶ`)...

Анна12061 29.11.2020 19:04

Для варенья из клубники на две части ягод берут 3 части сахара. Сколько сахара следует взять на 8 кг клубники...

Ромзэс1 29.11.2020 19:04

решить хоть что нибудь(КРОМЕ 4 ЗАДАНИЯ)...

ira231006 29.11.2020 19:04

Памагите 2+78+24+85-26+97-56-33+84-38-35+97+99-5...

krichilskaatтанюшка 29.11.2020 19:04

Вычисли значение дробного выражения: 8/13/1/13...

ssasin 29.11.2020 18:58

Артемон, Арлекин и Буратино решили вскладчину купить качели для всех друзей. Если бы Артемон увеличил свой вклад вдвое, общая сумма выросла бы на 67%. Если бы Буратино...

coffeepro80 29.11.2020 18:58

Пример 1. Определить угол между: y = -3 x + 7; y = 2 x + 1. Пример 2. Найти уравнение прямой, проходящей через две точки А(1, 2) и В(3, 4).Пример 3. Какая прямая проходит...

ilinovam 29.11.2020 18:57

с матешой! 1) Вычислить систему уравнений по формулам Коамера....

pakskina77p0byhm 29.11.2020 18:57

Заполни таблицу умоляю вас...

События a, b и c независимы; p(a) = 0,7, p(b) = 0,6 и p(c) = 0,3. найдите вероятность события a при усло- вии, что наступило событие a+b+c.

Популярные вопросы