Собрание из 12 человек избирает председателя,
секретаря и 3 членов
редакционной комиссии.
Сколькими
можно выбрать этих пятерых
Другие вопросы по теме Математика
Популярные вопросы
- Составьте блок-схему и программу нахождения стоимости 1,2,3,4,5,…,20 порций...
3 - ИСТОРИЯ заполнить таблицу всё что есть...
3 - Краткое описание трех водных географических объектов России-река, море, озеро(...
1 - Используйте притяжательные или структуру s, чтобы указать владение....
1 - Найдите радиус окружности описанной около треугольника со сторонами 10,12...
3 - Сделать задание по примеру 3....
1 - як здійснюється научіння у тварин??? ...
1 - У ребнека 7 лет чсс в норме...
1 - Это роятся белые пчелки! - говорила старая бабушка. Что она имела ввиду?...
2 - Впишите пропущенные числа: Масса Земли равна *10 т. Масса атома водорода...
3
Пошаговое объяснение:
Сколькими == найти число сочетаний
Так как все могут быть кем угодно, то найдем С(12, 5) = 12! / (5! * (12 - 5)!) = (12 * 11 * 10 * 9 * 8) / (5 * 4 * 3 * 2 * 1) = 792
Председателя и секретаря можно выбрать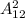
, а дополнительно еще трёх членов комиссии можно выбрать
Общее количество по правилу произведения есть