Сначала заданное выражение следует упростить и проинвертировать, а затем найти элементы множества P, выраженного через множества:

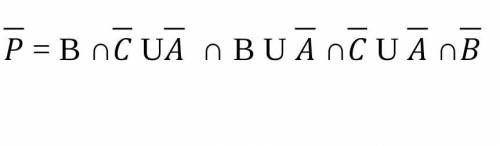
Другие вопросы по теме Математика
Популярные вопросы
- Check the boxes how well you can do these activities ...
1 -  Причини громадянських війн у Римській республіці...
1 - 1. Какое напряжение больше в повышающем трансформаторе и почему? 2. Какое напряжение...
3 - с текстом Перепишите текст, раскрывая скобки, вставляя, где это необходимо, пропущенные...
3 - Исторический диктант. Вакансии напиши нужное слово. 1. Великий китайский Курган...
1 - билет на автобус стоит 32 руб какое максимальное количество билетов можно будет...
2 - Упр.485А найдите антонимы...
1 - Мини сочинение на тему рахманинов рапсодия на тему поганини написать свои впечетления...
3 - Найти разложения вектора с= 3,1 по базису а= 2, 1 b=1;-1...
1 - 4. Прочитай. Выбери кульминационный эпизод. Подготовь выборочный пересказ. Главы...
1
Перед тем, как начать, давайте вспомним, что такое упрощение выражений и инверсия множеств.
Упрощение выражений - это процесс, в результате которого мы устраняем все возможные скобки, знаки операций и получаем наиболее простую форму выражения.
Инверсия (проинвертирование) множества - это процесс замены всех элементов множества на их дополнения относительно данного универсального множества.
Теперь перейдем к решению конкретной задачи:
1. Упрощение выражения:
- Выражение дано в виде объединения и пересечения множеств P, Q и R, поэтому сначала выполним операции пересечения и объединения внутри скобок.
- Внутри первой пары скобок у нас есть операция пересечения P и Q, поэтому найдем элементы, которые принадлежат и множеству P, и множеству Q.
- Множество P = {1, 2, 3, 4, 5}
- Множество Q = {3, 4, 5, 6, 7}
- Пересечение P и Q = {3, 4, 5}
- Вторая пара скобок содержит операцию объединения P и R, поэтому найдем все элементы, которые принадлежат хотя бы одному из этих множеств.
- Множество P = {1, 2, 3, 4, 5}
- Множество R = {4, 5, 6, 7, 8}
- Объединение P и R = {1, 2, 3, 4, 5, 6, 7, 8}
- Теперь объединим результаты полученных операций:
- Результат первой пары скобок (P пересекает Q) = {3, 4, 5}
- Результат второй пары скобок (P объединяет R) = {1, 2, 3, 4, 5, 6, 7, 8}
- Итоговое выражение = {3, 4, 5} пересекает {1, 2, 3, 4, 5, 6, 7, 8}
2. Инверсия множества:
- Инвертируем каждый элемент множества P относительно универсального множества U = {1, 2, 3, 4, 5, 6, 7, 8}:
- Инвертирование элемента 1: 1' = U\1 = {2, 3, 4, 5, 6, 7, 8}
- Инвертирование элемента 2: 2' = U\2 = {1, 3, 4, 5, 6, 7, 8}
- Инвертирование элемента 3: 3' = U\3 = {1, 2, 4, 5, 6, 7, 8}
- Инвертирование элемента 4: 4' = U\4 = {1, 2, 3, 5, 6, 7, 8}
- Инвертирование элемента 5: 5' = U\5 = {1, 2, 3, 4, 6, 7, 8}
- Итоговое проинвертированное множество P = {1' , 2', 3', 4', 5'}
Таким образом, после упрощения и инверсии выражения, мы получили искомое множество P = {1', 2', 3', 4', 5'}.
Надеюсь, это решение понятно и полезно для вас. Если у вас есть еще вопросы, буду рад помочь!