Случайная величина x принимает 2 равновозможных значения: x1 и x2 . ожидание m (x )= 4, дисперсия d(x ) = 1. найти x1 и x2 .

Ответы

EVETS1 10.09.2020 12:24

Каждому значению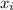 x_i соответствует значение вероятности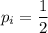 $p_i=\dfrac{1}{2}$

Закон распределения случайной величины X

Xi x1 x2

Pi 1/2 1/2

Х - дискретная случайная величина, тогда

$MX=\displaystyle \sum _ix_ip_i=\dfrac{x_1}{2}+\dfrac{x_2}{2}=\dfrac{1}{2}\left(x_1+x_2)=4$

$DX=MX^2-(MX)^2=\displaystyle \sum_ix_i^2p_i-4^2=\dfrac{1}{2}\left(x_1^2+x_2^2\right)-16=1$

Решим систему уравнений и найдем значения x1 и x2:

$\displaystyle \left \{ {{\dfrac{1}{2}(x_1+x_2)=4} \atop {\dfrac{1}{2}\left(x_1^2+x_2^2\right)-16=1}} \right.\Rightarrow\left \{ {{x_1+x_2=8} \atop {x_1^2+x_2^2=34}} \right.\Rightarrow\left \{ {{x_1+x_2=8} \atop {(x_1+x_2)^2-2x_1x_2=34}} \right.\\ \\ \\ \left \{ {{x_1+x_2=8} \atop {8^2-2x_1x_2=34}} \right.~~~\Rightarrow~~~\left \{ {{x_1+x_2=8} \atop {x_1x_2=15}} \right.~~\Rightarrow~~\left \{ {{x_1=3} \atop {x_2=5}} \right.~or~\left \{ {{x_1=5} \atop {x_2=3}} \right.$

ответ: 3 и 5 или 5 и 3.

ПОКАЗАТЬ ОТВЕТЫ

Мариночка010404 10.09.2020 12:24

сумма произведений значений величины на их вероятность - математич. ожидание.

Т.к. значения равновозможны. то вероятности их одинаковы. В сумме составляют 1, значит, каждая 0.5

0.5х₁+0.5х₂=4

Дисперсия - рассеивание, и ищем его как 0.5х₁²+0.5х₂²-4²=1

из первого уравнения х₁+х₂=8 найдем х₂=8-х₁ подставим во второе уравнение. Получим 0.5*((8-х₁)²+х₁²)-17=0

64-16х₁+2х₁²-34=0

30-16х₁+2х₁²=0

15-8х₁+х₁²=0, ПО теореме, обратной теореме Виета, корнями являются числа 3 и 5, значит, (х₁)₁=3 или (х₁)₂=5, а тогда соответственно (х₂)₁=5 или (х₂)₂=3.

ДОПОЛНЕНИЯ ДЛЯ ФОРМУЛ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ДСВ И ДИСПЕРСИИ ДСВ СМОТРИ ВО ВЛОЖЕНИИ.

оТВЕТ Х₁=3, Х₂=5

ИЛИ Х₁=5, Х₂=3