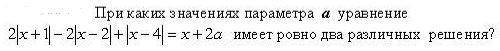
Математика: Сложная задача по математике

Сложная задача по математике

Ответы

КликКлак11 15.10.2020 15:41

(0; 1)∪{3}

Пошаговое объяснение:

Перенесём в левую часть x и рассмотрим функцию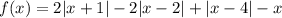 f(x)=2|x+1|-2|x-2|+|x-4|-x . Нули модулей: x = -1, x = 2, x = 4. Рассмотрим функцию относительно этих чисел:

$f(x)=\begin{cases}-2x-2, x$

Эту функцию получили так: в первом случае все модули превратили в скобки и перед ними поставили знак минус, упростили. Во втором — то же самое, но перед первым модулем ставим знак плюс. И так далее.

Построим график данной функции — строим прямые при указанных ограничениях (на рисунке отмечен зелёным). Посчитаем значения функции в точках "сгиба": f(-1) = 2·(-1)+2 = 0, f(2) = -2·2+10 = 6, f(4) = 2.

y = 2a — прямая, параллельная оси Ox. Если 2a < 0, то уравнение не имеет корней (нет пересечений), если 2a = 0, уравнение имеет один корень, если 0 < 2a < 2, уравнение имеет два корня, если 2a = 2, уравнение имеет бесконечно много корней, если 2 < 2a < 6, уравнение имеет три корня, если 2a = 6, уравнение имеет два корня, если 2a > 6, уравнение имеет один корень.

Подходящие значения параметра a: 0 < 2a < 2 ⇔ 0 < a < 1; 2a = 6 ⇔ a = 3.