скорость точки движущейся прямолинейно задана уравнением v=t^2-4t+3. Вычислите ее путь за 4-ую секунду
Другие вопросы по теме Математика
Популярные вопросы
- задача с++,массив,все числа меньше 500 увеличить на 100,вывести новый...
2 - решить 931 932 номер очень надо....
2 - составьте 1 предложение с каждым словом: horror romance comedy action...
3 - Краткая запист 6. Реши задачи.а) В летнем лагере группа из 64 детей...
2 - и объяснить принцип решений. 8 класс, окружности ...
1 - Из приведенного перечня солей выпишите отдельно средние, кислые, основные...
2 - Параграф 50 история 5 класс 1.) Заморские походы разоряли воинов-земледельцев....
2 - духовна траэкторія життя людини за повістю Чайка Джонатан Лівінгстон...
2 - У прямокутний трикутник, катети якого дорівнюють a і b, вписано коло,...
2 - Task 2. Make up 4 sentences using the words and write them correctly....
2
Скорость тела есть первая производная от пути. Значит, чтобы найти путь по известной зависимости скорости, нужно вычислить интеграл от скорости.
Так как нам нужен путь за четвертую секунду, то пределами интегрирования будут значения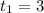 и
и 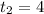 .
.
ответ: 4/3