1. Математика
  2. скорость движения тела изменяется

скорость движения тела изменяется по закону v(t)=6t^2+2t-3 найдите пройденный путь тела за 8 секунд от начала движения

почта6 почта6    2   19.06.2020 12:40    3

Ответы
alensolowiewa alensolowiewa  15.10.2020 14:27
Решение:

t_1=0 - это начало движения тела;

t_2=8 - время завершения движения тела;

То есть, чтобы найти пройденный путь тела за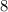 8 секунд от начала движения, нужно вычислить определённый интеграл:

\displaystyle \int\limits^8_0 {6{t}^{2}+2t-3} \, dt =\int\limits {6{t}^{2}} \, dt +\int\limits {2t} \, dt - \int\limits {3} \, dt =(2{t}^{3}+{t}^{2}-3t)\Big|^{8}_{0}= \\ \\ = 2\cdot{8}^{3}+{8}^{2}-3\cdot8-(2\cdot0-3\cdot0)={2}^{10}+64-24-0=1088-24=\boxed{1064}Использованные формулы:

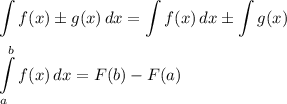
\displaystyle \int\limits {f(x)\pm g(x)} \, dx=\int\limits {f(x)}\, dx \pm \int\limits {g(x)} \\ \\ \int\limits^b_a{f(x)} \, dx =F(b)-F(a)

ответ: \Large{\boxed{1064}}
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Sanya030814 Sanya030814  23.12.2020 12:02
ПАЦАНЫ У КОГО СЕГОДНЯ СОЧ ПО МАТЕШЕ(КЛАСС 5)ПИШИТЕ СЮДА Я УЖЕ ВСЁ СДЕЛАЛ НА 5!​...
Nastyaaaaaa34 Nastyaaaaaa34  23.12.2020 12:02
Отношение количества мальчиков к количеству девочек в классе 1 : 4. Какую часть мальчики составляют от общего количества класса Очень нужно!​...
dima11232 dima11232  23.12.2020 12:02
Сократите дроби 9/15, 24/36,. 9/54​...
Незнаюзачемтутник Незнаюзачемтутник  23.12.2020 12:02
Определить массу приготовления и количество отходов при холодной обработке 5 кг картофеля в сентябре...
fanaidap fanaidap  23.12.2020 12:02
кто и все решит тому закину на киви ​...
superschool1 superschool1  23.12.2020 12:02
вычислите я понимаю я сам должен но если сможете тут тоже матем. Соч 5 класс дам 20 честно​...
larisa2912200 larisa2912200  23.12.2020 12:02
К сплаву 600г , содержащему 60%, добавили 400 г олова. найди процентное содержание олова в сплаве. С решением ​...
BlackGus007 BlackGus007  23.12.2020 12:02
Из вершины прямого угла MNK (см рис.) проведены два луча ND и NE так, что ∠MND = 64°, ∠KNF = 48°. Вычислите градусную меру угла DNF....
messaivi messaivi  23.12.2020 12:03
Найдите неверное утверждение. (16) 1.Краткие имена прилагательные отвечают на вопросы каков? какова?каково?2. Краткие имена прилагательные изменяются по родам, падежам,...
Frienden Frienden  18.09.2019 09:40
25 плиток 40×40 сколько это квадратов ?...

Популярные вопросы