Сколько существует несократимых дробей с числителем x и знаминателем 16 при которых верно неравенство
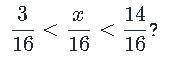
Другие вопросы по теме Математика
Популярные вопросы
- Объедините в три группы с одной и той же орфограммой в корне. указка, прелестный,...
2 - Найдите неизвестный член пропорции 4,5 разделить на 0,6 равно икс разделить на...
3 - 4. вставь пропущенные слова в правильной форме. use: take swim use hunt carry hide...
1 - Из какой сказки эти предложения. всего опаснее были ясные заездные ночи . объясните...
2 - На c++ даны два числа d и l. требуется найти первые 15 натуральных чисел, не меньших,...
1 - Как изображают народ в свомх произведениях некрасов и лесков?...
3 - Помгите написать сочинение по казахскому на тему уақыт . заранее !...
3 - Скажите, , как посчитать? 0,018/6*10^-23...
1 - Перевести шестнадцатеричное число в восьмтричную систему счисления: facb16...
3 - 1) назовите вещества : znl2 , h2so3 , ca(oh)2 , al2(co3)3 , fe2o3 2) запишите формулы...
2
1. Перепишем неравенство в виде дроби: (x + 5)/(16 - x) > 1.
2. Приведём обе части дроби к общему знаменателю 16 - x: (x + 5)/(16 - x) - 1 > 0.
3. Упростим левую часть выражения: (x + 5 - (16 - x))/(16 - x) > 0.
4. Проведём арифметические операции в числителе: (x + 5 - 16 + x)/(16 - x) > 0.
5. Упростим числитель: (2x - 11)/(16 - x) > 0.
6. Для нахождения решений данного неравенства рассмотрим знаки числителя и знаменателя.
a) Числитель 2x - 11 положителен, когда 2x - 11 > 0. Решая это неравенство, получаем: x > 5.5.
b) Знаменатель 16 - x положителен, когда 16 - x > 0. Решая это неравенство, получаем: x < 16.
7. Таким образом, для того чтобы неравенство (x + 5)/(16 - x) > 1 выполнялось, нужно, чтобы x принадлежало интервалу (5.5, 16).
8. Поскольку x является числителем дроби, а знаменатель равен 16, то ответом на вопрос является количество целых чисел на интервале (5.5, 16). Мы можем округлить числа до ближайших целых чисел, получая варианты для числителя: 6, 7, 8, 9, 10, 11, 12, 13, 14, 15. Таким образом, существует 10 несократимых дробей с числителем x и знаменателем 16, которые удовлетворяют данному неравенству.
Вот подробное решение задачи. Если у тебя остались какие-либо вопросы, не стесняйся задать их!