Сколько различных трехзначных чисел можно составить из цифр 3, 0 и 6, если цифры в одном числе не могут повторяться? A) 3
B) 4
C) 5 D) 6

В) 4

Пошаговое объяснение:

1-ый

На первую позицию можно подставить любую цифру, кроме 0 (т.к на 0 число не может начинаться) - 2.

На вторую позицию можно подставить оставшуюся цифру и 0 (ноль) - 2.

На третью позицию можно подставить 1 оставшуюся цифру - 1.

2*2*1=4*1=4 числа

Для трехзначного числа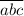 вместо цифры может стоять одна из двух цифр: 3 или 6 (цифра 0 не может находится в наивысшем разряде в трехзначном числе); вместо цифры 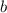может стоять одна из двух оставшихся цифр, включая 0; вместо цифры может стоять одна оставшаяся цифра.

Таким образом, по правилу комбинаторного произведения имеем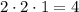 таких трехзначных числа.

Из 3 цифр можно образовать 3 перестановки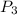 . Однако трехзначное число не может начинаться с нуля. Перестановки, начинающиеся с цифры 0,  а следовательно, не удовлетворяющие условию задачи, будет 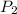. Итак, искомое количество трехзначных чисел равно:

ответ: 4