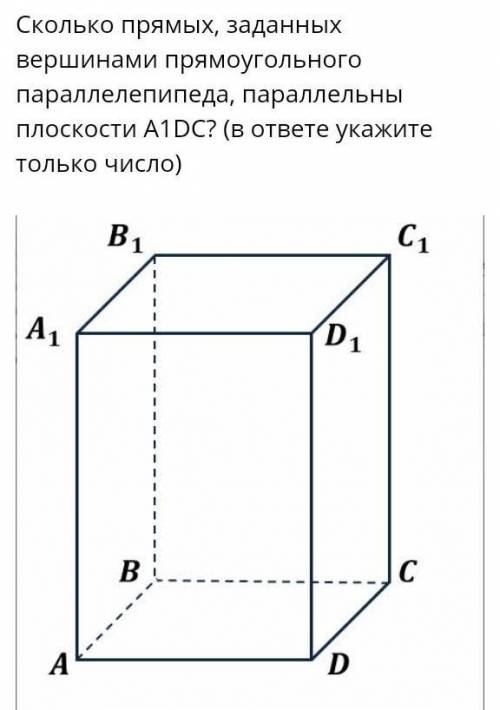
Сколько прямых, заданных вершинами прямоугольного параллелепипеда, параллельны плоскости A1DC? (в ответе укажите только число)​

Для решения этой задачи, нам нужно понять, какие прямые в параллелепипеде параллельны плоскости A1DC. Плоскость A1DC является горизонтальной плоскостью, проходящей через вершины A1, D и C параллелепипеда. Чтобы узнать, какие прямые параллельны этой плоскости, мы можем рассмотреть их проекции на эту плоскость. Проекция прямой на плоскость - это линия, которую получаем, если "опускаем" перпендикуляр из каждой точки прямой на эту плоскость. Если две прямые имеют одинаковые проекции на плоскость, то эти прямые параллельны этой плоскости. Теперь рассмотрим прямоугольный параллелепипед, заданный данными вершинами. Заметим, что на рисунке приведены прямые, образующие ребра параллелепипеда и пересекающие плоскость A1DC. Давайте пронумеруем эти прямые для ясности: 1. AB 2. AD 3. AE 4. BC 5. BD 6. DE 7. CF 8. FG 9. FH 10. DC 11. AB1 12. GD 13. HE Теперь давайте определим, какие прямые параллельны плоскости A1DC, а какие - нет. Прямые, заданные вершинами параллелепипеда, параллельны плоскости A1DC, если их проекции на плоскость A1DC одинаковы. Рассмотрим каждую прямую по отдельности: 1. Проекция прямой AB на плоскость A1DC обозначим AB'. АB' - это отрезок перпендикуляра, опущенного из точки B на плоскость A1DC. Видно, что прямая AB не параллельна плоскости A1DC, так как AB' и A1C не параллельны. 2. Аналогично, прямая AD не параллельна плоскости A1DC, так как ее проекция AD' и A1C не параллельны. 3. Поступим так же и с остальными прямыми. 4. Проекции AE и DE на плоскость A1DC обозначим AE' и DE'. Видно, что прямые AE и DE параллельны плоскости A1DC, так как их проекции AE' и DE' параллельны A1C. 5. Аналогично, прямые BC и DC параллельны плоскости A1DC, так как их проекции BC' и DC' параллельны A1C. Таким образом, получаем, что всего 5 прямых, заданных вершинами прямоугольного параллелепипеда, параллельны плоскости A1DC: AE, DE, BC, DC, AB1. Ответ: 5 прямых.