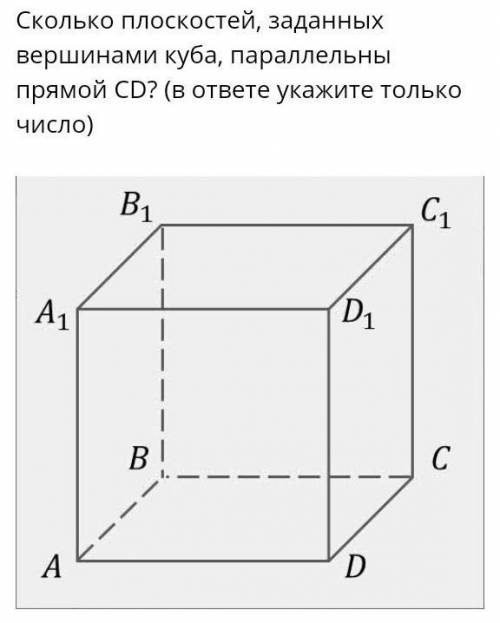
Сколько плоскостей, заданных вершинами куба, параллельны прямой CD? (в ответе укажите только число) ​

3 плоскости или я ошибаюсь если нет так то поправьте меня

Для решения этой задачи, нам нужно определить, какие из вершин куба лежат на прямой CD, и затем посчитать количество плоскостей, проходящих через эти вершины и параллельных CD.

Для начала, давайте рассмотрим, какие вершины куба лежат на прямой CD. Изображение показывает, что вершины A, B, C и D лежат на прямой CD.

Теперь, посмотрим на плоскости, которые проходят через вершины куба и параллельны CD. Каждую из данных вершин мы можем соединить с вершинами, которые лежат на параллельных сторонах куба и также лежат на прямой CD.

Следуя этому методу, мы видим что:

- Вершина A может быть соединена с B, F и E.
- Вершина B может быть соединена с A, C и G.
- Вершина C может быть соединена с B, D и H.
- Вершина D может быть соединена с C, A и O.

Суммируя, мы получаем 4 плоскости, проходящие через данные 4 вершины A, B, C и D и параллельные прямой CD.

Таким образом, ответ на данную задачу составляет 4 плоскости.