Сколько есть вырезать две клетки из шахматной доски так, чтобы оставшуюся часть модно было разрезать на доминошки (прямоугольники 1 * 2)?

1024

Пошаговое объяснение:

1) Т.к. соседи клетки по стороне имеют противоположный цвет (1), то доминошка накрывает по одной клетке черного и белого цвета.

2) Если вырезать две клетки одного цвета, кол-во белых и черных клеток станет неравным -> накрыть доминошками не получится

3) Докажем, что при вырезании любой пары белой и черной клеток доску можно накрыть доминошками.

Сначала построим замкнутый путь, обойдя каждую клетку доски по одному разу (пример на изображении, для удобства восприятия красным обозначен путь, синим - разделители). Из (1) очевидно следует, что любой такой путь (он НЕ единственный) состоит из чередующихся черных и белых клеток.

Вырезав две клетки, мы разобьем путь на два отрезка (нулевая длина также возможна). Т.к. клетки на пути чередуются, а вырезаем мы 2 клетки разных цветов, то "расстояние" между вырезами на пути (кол-во клеток между вырезами, если считать их в порядке обхода по красной линии - по пути) будет четным. А значит "длины" обоих отрезков пути (кол-во клеток в их составе) четны. А тогда мы всегда можем замостить из доминошками, если будем класть их друг за другом вдоль пути.

Ч.т.д.

4) Осталось посчитать число вырезать одну черную и одну белую клетки из доски: клеток каждого цвета по 32, а значит число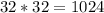 . Это и есть искомый ответ