Сколькими нулями заканчивается произведение всех чисел от 1 до 100?

Подсчитаем сколько раз приходится число 2 в факториал 100

В разложении на простые множители числа 100! двойка встречается ровно 97 раз.

Теперь подсчитаем сколько раз приходится число 5 в факториал 100

Число 5 встречается ровно 24 раза.

Значит,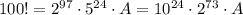 , где А - некоторый множитель. И как видим, данное произведение оканчивается 24 нулями.

ответ: 24 нулями.

1) В произведении от 1 до 100 есть 9 чисел, оканчивающихся 0 (10,20,30,40,50,60,70,80,90),  и число 100 с двумя нулями.

2) Кроме того   5 · 2 = 10

Каждое умножение 5 и 2 даст на конце 0. Числа, которые оканчиваются на 5 :  5,15,25,35,45,55,65,75,85,95  -  всего 10 чисел.

3) Числа, которые имеют по два множителя 5 : 25,50,75  - всего 3.

От 1 до 100 есть  9+2=11 нулей  и  ещё 10+3=13  пятёрок, для которых найдётся нужное количество двоек, например

64 · 32 · 4 = 2⁶ · 2⁵ · 2² = 2¹³

11 + 13 = 24

ответ : 24 нуля