Сколькими можно выбрать четыре различных натуральных числа из отрезка [1; 53] так,чтобы их сумма была четной (наборы отличающиеся только порядком чисел,являются одинаковыми)
Другие вопросы по теме Математика
Популярные вопросы
- Алхимик решил приготовить волшебный эликсир. В банке имеется 10 литров...
1 - Перепишите, вставляя пропущенные буквы и раскрывая скобки.Устно объясните...
1 - Заполнить таблицу ФИЗИКА 8 КЛАСС...
1 - По данным рис. найдите отрезок,обозначенный через x (0 — центр окружности)...
1 - Проанализировать стихотворение М. В. Исаковского «Враги сожгли родную...
1 - Під час хімічної взаємодії розчину сульфатної кислоти H2SO4 з барій...
3 - Контрольна робота 7 за темою Числівник 6 класс Числівниками є всі слова...
1 - На складе было 90 меш.муки. до обеда продали 30 меш, а после обеда 32...
3 - Имя Лидера восставших крестьян в Англии....
3 - В 2017 году на остров вблизи полуострова Аляски привели 6 паредведей,...
2
146575
Пошаговое объяснение:
4 числа с нечетной суммой можно выбрать такими, что:
1) все 4 числа четные
2) все 4 числа нечетные
3) 2 четных, 2 нечетных
Всего четных чисел на отрезке [1;53] равно 26, нечетных 27.
1) Число выбрать 4 четных числа без учета порядка равно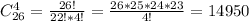
2) Число выбрать 4 нечетных числа без учета порядка равно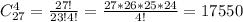
3) Число выбрать два четных равно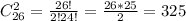
Число выбрать два нечетных числа равно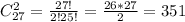
Так как множества четных и нечетных чисел не пересекаются, то число выбрать 2 четных и 2 нечетных равно произведению числа То есть 325*351=114075.
Сложим все результаты из трех пунктов: 14950+17550+114075=146575