Скільки різних слів можна одержати, переставляючи букви слова «ліцей»? 2.Скількома в команді спортсменів з 10 чоловік можна розподілити 3 призових місця? 3. У ящику лежать 20 червоних, 10 жовтих і 5 зелених яблук. Навмання вибирають 7 яблук. Яка ймовірність того, що серед вибраних яблук є 2 червоних, 4 жовтих і 1 зелене?
Другие вопросы по теме Математика
Популярные вопросы
- Тау бедеринин адам омирине кауиптилиги кандай ?...
2 - Кусок льда массой 1 кг нагревают от −16°C до −3°C, затрачивая при этом количество...
3 - 1) Запишите в виде несократимой дроби:72. 6090 105...
1 - 2. Укажите заряды атомных ядер, количество электронов и относительную атомную массу...
3 - квадрат стороной 5 см распилили на квадратики по 1 см из полученых квадратиков...
1 - 188 Постройте устно текст-рассуждение, ответив на вопрос: «Почему рас- ІІДве недели...
1 - В каком из примеров правильно употреблено прилагательное с «НЕ» слитно? Неважная,...
2 - 21. Найдите значение выражения:...
2 - Можете написать примеры из помана Дубровский доказательство, что он был разбойником...
3 - ТЕКСТ ЗАДАНИЯ Даны точки А (-3;2), В (1;0), C(-2; - 4). Определите координаты точки...
2
1. У слові "ліцей" є 5 букв, які можна переставляти в будь-якому порядку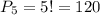
Відповідь: 120 слів.
2. Перше місце дістанеться одному з 10 спортсменів, друге місце — одному з 9 спортсменів, бо один уже має своє призове місце, і т. д.
Тобто маємо розміщення з 3 елементів по 10:
Відповідь в.
3. Вибір 2-х червоних яблук з 20: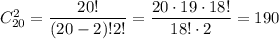 в.
в.
Вибір 4-х жовтих яблук з 10: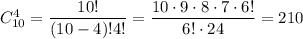 в.
в.
Вибір 1-го зеленого яблука з 5: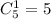 в.
в.
Вибір 2 + 4 + 1 = 7 яблук з 20 + 10 + 5 = 35: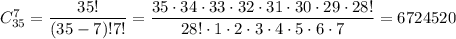
Нехай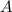 — подія, яка полягає в тому, що серед вибраних яблук з ящику є 2 червоних, 4 жовтих і 1 зелене.
— подія, яка полягає в тому, що серед вибраних яблук з ящику є 2 червоних, 4 жовтих і 1 зелене.
Відповідь: 0,03.