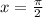Sin2x + cosx = 0 на промежутке (0,п)
Другие вопросы по теме Математика
Популярные вопросы
- Задайте формулою пряму пропорційність, графік якої проходить через точку М (-9;3)....
2 - Расстояние между точечными зарядами q1 и q2 составляет 0,15 метров.Определите напряжённость...
2 - Наведіть приклади правовідносин, які регулюються кримінальним правом і проаналізуйте...
1 - I. Use Possessive case. Перефразуйте, використовуючи присвійний відмінок іменника...
3 - ЗАРАНЕЕ Соотнесите условия обособления (необособления) членов предложения с примерами....
3 - Чип и Дейл купили одинаковое количество бананов. Когда Чип съел 47 бананов, а Дейл...
3 - Найдите на рисунке 119 пары перпендикулярных прямых и запишите их...
1 - Судно, занурено в воду по ватерлінію, має масу 20000кг. Який об єм води воно витісняє?...
3 - ЗАДАНИЕ № 1. Запишите слова парами, чтобы в каждой паре было слово с безударной...
3 - Электрон, проходя между обкладками конденсатора электронно-лучевой трубки, отклоняется...
1
Первая серия на заданном отрезке дает единственное решение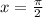 при
при 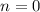 . Вторая же серия на данном отрезке (с учетом того, что
. Вторая же серия на данном отрезке (с учетом того, что 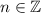 ) вообще не дает корней.
) вообще не дает корней.
ОТВЕТ: