Sin x - корень из 3 cos x = корень из трёх решите

Допустим, 1/2 и √3/2 это sin и cos какого-то угла. Это возможно если выполняется основное тригонометрическое тождество, то есть когда этот угол определён на тригон. круге. Проверяем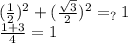 Да всё верное, обозначим этот угол как α=arcsin(1/2)+2pi*n, n∈Z. Стоит отметить, что т.к. и синус и косинус этого угла положительны, то этот угол может лежать исключительно в 1 четверти.

Тогда у нас есть -sinα*sinx+cosα*cosx= -√3/2

Левую часть можно представить как косинус суммы.

cos(α+x)= -√3/2.

cos(arcsin(1/2)+2pi*n+x)= -√3/2, n∈Z. 2Pi*n можно сократить так как это целые круги и значение косинуса ни как не поменяется. И тогда сразу берём arccos.

arcsin(1/2)+x= ±5pi/6+2pi*k, k∈Z. Раскрываем arcsin т.к. это табличное значение и мы его знаем, ну я точно.

x= ±5pi/6-pi/6+2pi*k, k∈Z.

k∈Z.

ответ: x={-pi+2pi*k; 2pi/3+2pi*k}. k∈Z.