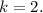Сфункцией и её графиком. подробно и с объяснением, .
Другие вопросы по теме Математика
Популярные вопросы
- Прочитайте текст Запишите его на противоположном берегу озера подходил...
3 - 0000000000000000000000000000...
2 - Менің дағыстаным әңгімесінде ана не диді? қысқартып айтасындарма) Өтініш...
3 - Катер по течению реки от пристани Победа до пристани Абрау-дюрсо за 3...
1 - Крізь воду кількістю Речовини 10 моль пропустили електричний струм. Обчісліть...
2 - Сочинение Как вы понимаете, что такое сочувствие и сострадание по плану...
2 - Что значит «знать язык» и «владеть речью»? Распредели данные словосочетания...
1 - 21. Какие дисциплины включал пентатлон – древнегреческое пятиборье? 1....
3 - Рим империясындагы дагдарыс кориниси...
3 - 7. Установіть відповідність між реченням та його характеристикою: 1....
3
Вычислим для начала область определения функции: функция существует когда знаменатель дроби не обращается к нулю
ООФ: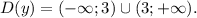
Упростим функцию:
Графиком функции есть прямая, проходящая через точки (0;1), (-1;-1)
Функция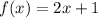 не имеет общих точек с прямой
не имеет общих точек с прямой 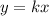 в том случае, когда прямая
в том случае, когда прямая 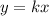 будет проходить через выколотую точку (3;7), т.е. подставляя их координаты, мы получим
будет проходить через выколотую точку (3;7), т.е. подставляя их координаты, мы получим
Если приравнять функции, т.е.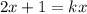 , тогда
, тогда
То при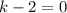 откуда
откуда 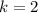 графики функций общих точек не имеют. Если понять как графически делать, то очевидно, что если две прямые параллельны, то графики не имеют общих точек, а прямые параллельны в том случае, когда их угловые коэффициенты равны, т.е. k = 2
графики функций общих точек не имеют. Если понять как графически делать, то очевидно, что если две прямые параллельны, то графики не имеют общих точек, а прямые параллельны в том случае, когда их угловые коэффициенты равны, т.е. k = 2
ответ: при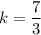 и
и