Сэкзамера
спортсмен, стартуя с одного конца бассейна, доплывает до другого конца бассейна, поворачивает и плывёт обратно. в тот момент, когда он поворачивает, по соседней дорожке навстречу ему выплывает другой спортсмен, который проплывает расстояние от одного до другого конца бассейна за 36 секунд. первый спортсмен вернулся к месту своего старта через 25 секунд после того, как поравнялся со спортсменом, плывшим ему навстречу. предполагая, что скорость спортсменов всё время была постоянной, определите, через сколько минут после начала своего заплыва первый спортсмен вернулся к месту старта.
объясните максимально подробного, прямо как для тупого. я в край не понимаю объяснение этой на самом экзамере. скопированные/переписанные решения будут удалены. ответ должен быть 1.5.
Другие вопросы по теме Математика
Популярные вопросы
- Постройте графики прямой пропорциональности:1) у = 2х;х10 12 4) у = -2,5х;у 12)...
3 - С 23 учеников 9 класса 1 имеет высокий уровень, 5 - достаточный, 12 - средний, а...
1 - 1. Пять гостей рассадить на 5 свободных мест за столом. Сколько возможно вариантов....
2 - Во Сколько прелестных дев окружала Ратмира.Поэма Руслан и Людмила....
1 - Послушайте древнеегипетский миф. Почему Ра открыл свою тайну? Найдите в тексте фрагмент,...
1 - В каком времени стоит слово было...
3 - Выясни вид заданных событий (возможно несколько вариантов ответа): при бросании...
2 - Во с ответами на тему тихая моя родина Паустовский...
1 - Л.р по физике Исследование зависимости угла переломления света от угла паданения...
2 - Может ли частное оказаться больше делимого? если может, приведите пример....
2
Пусть первый спортсмен вернулся к месту старта через x минут после начала своего заплыва. x мин = 60x секунд.
Значит, от одного другого конца бассейна первый доплывает за 60x:2 = 30x секунд.
Пусть длина дорожки y метров (можно и за единицу принять - всё равно сократится потом).
Тогда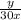 м/с скорость первого пловца,
м/с скорость первого пловца, 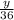 м/с - скорость второго.
м/с - скорость второго.
От конца дорожки до места встречи первый доплыл за 30x-25 секунд. Второй от начала дорожки до места встречи доплыл за то же время, т.к. начали встречное движение одновременно.
За это время первый проплыл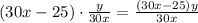 метров, второй
метров, второй 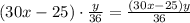 метров. В сумме проплыли расстояние, равное длине дорожки, то есть
метров. В сумме проплыли расстояние, равное длине дорожки, то есть
ответ: первый спортсмен вернулся к месту старта через 1,5 минуты после начала своего заплыва