1. Математика
  2. сделайте задания по математике.

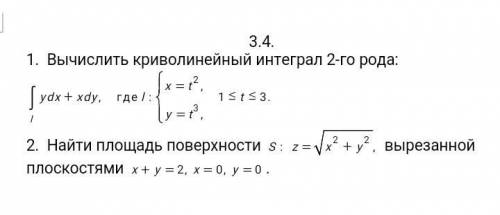
сделайте задания по математике. На последней фото задача 5


сделайте задания по математике. На последней фото задача 5
сделайте задания по математике. На последней фото задача 5
сделайте задания по математике. На последней фото задача 5

SANH1L SANH1L    3   27.06.2021 13:04    1

Ответы
anastasiabobilevich anastasiabobilevich  27.07.2021 13:43

x∈ (-n-2;-n+2]

Пошаговое объяснение:

a_n=\frac{1}{2^n}

Вычислим радиус сходимости:

R= \lim_{n \to \infty} \frac{a_n}{a_{n+1}}\\R= \lim_{n \to \infty} \frac{\frac{1}{2^n} }{\frac{1}{2^{n+1}} } = \lim_{n \to \infty} \frac{2*2^n}{2^n}=2

Находим область сходимости степенного ряда:

x_1=-n-2\\x_2=-n+2\\

x∈(-n-2; -n+2)

Остаётся проверить сходимость ряда на концах данного интервала.

При х = -n-2 мы получим следующий ряд:

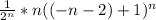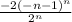
∑\frac{1}{2^n}*n((-n-2)+1)^n=∑\frac{-2(-n-1)^n}{2^n}

Рассмотрим первых 3 члена данного ряда: -2; 1/8; -128

Данный ряд будем исследовать по признакам Лейбница

\lim_{n \to \infty} \frac{2(-n-1)^n}{2^n} \\2\frac{1}{8}

Как видим, выполняется лишь второе условие Лейбница, а значит ряд расходится => x=-n-2 является точкой расходимости.

Рассматриваем второй конец x=-n+2

Получаем следующий ряд

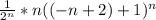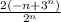
∑\frac{1}{2^n}*n((-n+2)+1)^n=∑\frac{2(-n+3^n)}{2^n}

Тут исследуем по признакам Даламбера

\lim_{n \to \infty} \frac{u_{n+1}}{u_n}=q

q=1 - неопределённость, т.к. при q>1 ряд расходится, а при q<1 - сходится.

\lim_{n \to \infty} \frac{\frac{2(-(n+1)+3)^{n+1}}{2^{n+1}} }{\frac{2(-n+3)^n}{2^n} }= \lim_{n \to \infty} \frac{2^{(-n+2)}^{n+1}}{2^{(-n+3)}^n} *\frac{2^n}{2^{n+1}}= \lim_{n \to \infty} \frac{2^{-n+2}^{n+1}}{2*2^{-n+3}^n} =\frac{1}{2}

q<1 , а это значит, что ряд сходится. х=-n+2 является точкой сходимости.

Тогда данный степенной ряд является сходящимся при x∈ (-n-2;-n+2]

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
bilpi bilpi  18.07.2019 12:20
График линейной функции y=kx+b проходит через точки a(2; 3) и b(-4; 6).задайте формулой данную функцию. а) y=-0.5x+4 б)y=-0.5x-4 в)y=0.5x-4 г)y=0.5x+4...
graf2231 graf2231  18.07.2019 12:20
При каких значениях x 0,5x-6 ,больше выражения 7х+13,5...
Demix485 Demix485  18.07.2019 12:20
Na tri poyezda : skoriy,passajirskiy i elapses iz moskvi v pskov ,prodano 1040 biletov.na skoriy i passajirskiy poyezda prodano 746 biletov, na passajirskiy poyezd i...
08077987979 08077987979  18.07.2019 12:20
Пассажир метро спускается по движущемуся эскалатору за 24 секунды если он пойдет по недвижимому эскалатору с той же скоростью спуститься вниз за 42 секунды за какое...
a24027679 a24027679  18.07.2019 12:20
Из двух посёлков,находящихся друг от друга на расстоянии 17 км,одновремнно в противоположные направлениях вышли два лыжника.через некоторое время они остановились.в...
Артёмка12097 Артёмка12097  18.07.2019 12:20
Укажите все целые, принадлежащие исловому промежутку: 1) (2; 7,5]; 2) [-21; -17]; 3) [ 12,3; 13,1]; 4) [ -7 1/3; -2,99] 5) (-1; 4)....
artur282 artur282  18.07.2019 12:20
Какое из данных ниже выражений при любых значениях k равно степени 5^3-k...
ник3999 ник3999  18.07.2019 12:20
Спортивная яхта идет со скоростью18 км/ч. через два часанй в вдогонку выходит вторая яхта и идет со скоростью 27 км/ч. через сколько часов вторая яхта догонит первую?...
Cyndyma Cyndyma  18.07.2019 12:20
Маша взялась ухаживать за курами и кроликами. всего у её подшевных 35 голов и 94 ноги.сколько у маши кур и сколько кроликов?...
shvbur75 shvbur75  18.07.2019 12:20
Вхозяйстве от каждой коровы получали в среднем по 14 л молока в сутки. сколько литров молока получат в этом хозяйстве от 10 коров за 7 суток....

Популярные вопросы