Сделайте математику 1 курс​ Определение 1. Функцию называют обратимой, если любое свое значение она принимает только в одной точке множества X.
Теорема. Если функция монотонна на множестве X, то она обратима.
Доказательство:

Пусть функция y=f(x) возрастает на множестве Х и пусть х1≠х2 – две точки множества Х.

Для определенности пусть х1< х2. Тогда из того, что х1 < х2  в силу возрастания функции следует, что f(х1) < f(х2).

Таким образом, разным значениям аргумента соответствуют разные значения функции, т.е. функция обратима.

Аналогично доказывается теорема в случае убывающей функции.

Перед тем как сформулировать определение обратной функции учитель просит учащихся определить, какая из предложенных функций обратима? На интерактивной доске показаны графики функций (рис. 3, 4) и записаны несколько аналитически заданных функций:
 а)   б) 
Рис. 3 Рис. 4
в) y = 2x + 5;  г) y = - + 7.
Замечание. Монотонность функции, является достаточным условием существования обратной функции. Но оно не является необходимым условием.
2) Понятие обратной функции. Алгоритм составления обратной функции.
Определение 2. Пусть обратимая функция y=f(x) определена на множестве Х и область ее значений Е(f)=Y. Поставим в соответствие каждому y из Y то единственное значение х, при котором f(x)=y. Тогда получим функцию, которая определена на Y, а Х – область значений функции. Эту функцию обозначают x=f -1(y),  и называют обратной по отношению к функции y=f(x),.
Затем учитель знакомит учащихся со нахождения обратной функции, заданной аналитически.
Алгоритм составления обратной функции для функции y=f(x), .

Убедиться, что функция y=f(x) обратима на промежутке Х.

Выразить переменную х через у из уравнения y=f(x), учитывая при этом, что .

В полученном равенстве поменять местами х и у. Вместо х=f -1(y) пишут y=f -1(x).

На конкретных примерах учитель показывает как использовать данный алгоритм.
Пример 1. Показать, что для функции y=2x-5 существует обратная функция, и найти ее аналитическое выражение.
Решение. Линейная функция y=2x-5 определена на R, возрастает на R и область ее значений есть R. Значит, обратная функция существует на R. Чтобы найти ее аналитическое выражение, решим уравнение y=2x-5 относительно х; получим .  Переобозначим переменные, получим искомую обратную функцию  . Она определена и возрастает на R.
Пример 2. Показать, что для функции y=x2, х ≤ 0 существует обратная функция, и найти ее аналитическое выражение.
Решение. Функция непрерывна, монотонна в своей области определения, следовательно, она обратима. Проанализировав области определения и множества значений функции, делается соответствующий вывод об аналитическом выражении для обратной функции, которая имеет вид .
3) Свойства взаимно обратных функций.
Свойство 1. Если g – функция обратная к f, то и f – функция обратная к g (функции взаимно обратные), при этом D(g)=E(f), E(g)=D(f).
Свойство 2. Если функция возрастает (убывает) на множестве Х, а У – область значений функции, то обратная функция возрастает (убывает) на У.
Свойство 3. Чтобы получить график функции , обратной по отношению к функции , надо график функциипреобразовать симметрично относительно прямой у=х.
Свойство 4. Если нечетная функция обратима, то обратная ей тоже нечетная.
Свойство 5. Если функции f(x) и взаимно обратные, то для любого справедливо , а для любого справедливо .
Пример 3. Построить график функции обратной , если это возможно.
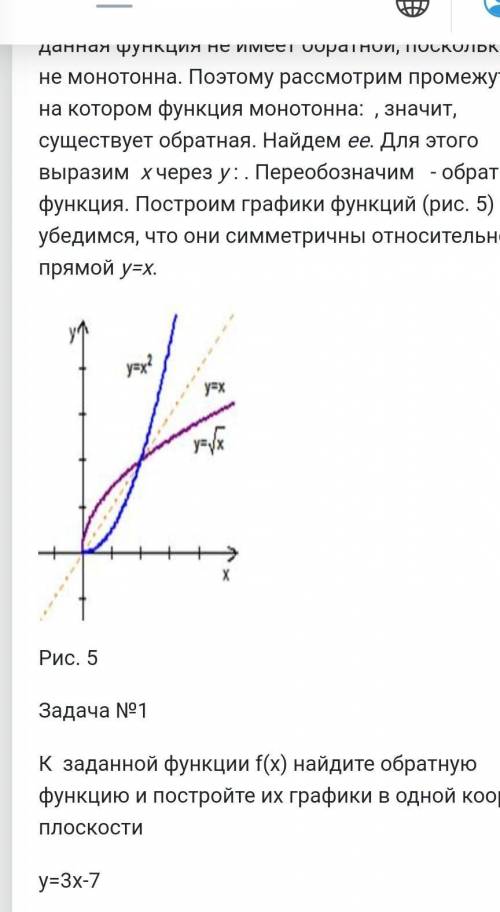
Решение. На всей своей области определения данная функция не имеет обратной, поскольку она не монотонна. Поэтому рассмотрим промежуток, на котором функция монотонна:  , значит, существует обратная. Найдем ее. Для этого выразим  x через y : . Переобозначим   - обратная функция. Построим графики функций (рис. 5) и убедимся, что они симметричны относительно прямой y=x.

Рис. 5
Задача №1
К  заданной функции f(x) найдите обратную функцию и постройте их графики в одной коорд плоскости
у=3х-7
у=2-3х
у=2х+1
у=3-2х

Alihan184    1   11.09.2020 21:57    8