1. Математика
  2. сделать самостоятельную работу

сделать самостоятельную работу по алгебре​


сделать самостоятельную работу по алгебре​

popdaniela820 popdaniela820    2   22.03.2021 16:21    1

Ответы
Зефирка1907 Зефирка1907  21.04.2021 16:36

1) 15

2) 14

3) 12

4) 56

5) -

Пошаговое объяснение:

  №1

формулы арифметической прогрессии:

  a_{n} =\frac{a_{n+1}+a_{n-1}}{2}     свойство

 d=a_{n+1}-a_{n}        разность

 a_{n}=a_{1}+(n-1)*d    формула n-ого члена

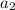найдём a_{2} чтобы найти "разность (d)    

a_{n} =\frac{a_{n+1}+a_{n-1}}{2} \\ a_{2} =\frac{a_{3}+a_{1}}{2}=\frac{6+(-3)}{2} =1,5

d=a_{n+1}-a_{n}\\d=a_{3}-a_{2} = 6-1,5=4,5

теперь сможем найти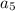 a_{5}

a_{n}=a_{1}+(n-1)*d\\a_{5}=a_{1}+(5-1)*d = -1,5+(5-1)*4,5 = 15

ответ: 15

 №2

\left \{ {{a_{2}+{a_{4}=16 } \atop {{a_{1}*{a_{5} =28 }} \right.      

распишем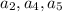 {a_{2}, {a_{4} , {a_{5} через формулу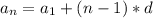 a_{n}=a_{1}+(n-1)*d

a_{2}=a_{1}+(2-1)*d=a_{1}+d\\a_{4}=a_{1}+(4-1)*d=a_{1}+3d\\a_{5}=a_{1}+(5-1)*d=a_{1}+4d

вставим их в систему

\left \{ {{a_{2}+{a_{4}=16 } \atop {{a_{1}*{a_{5} =28 }} \right. ⇒ \left \{ {{a_{1}+d+{a_{1}+3d=16 } \atop {{a_{1}*({a_{1}+4d) =28 }} \right. ⇒ \left \{ {2{a_{1}+4d=16 } \atop {{a_{1}^{2} *4{a_{1}d =28 }} \right. ⇒ \left \{ {{a_{1}=8-2d } \atop {(8-2d)^2+4(8-2d)*d=28} \right.

(8-2d)^2+4(8-2d)*d=28\\(8-2d)^2+4(8-2d)*d-28=0\\64-32d^2+4d^2+32d-8d^2-28=0\\-4d^2+36=0 /(-4)\\d^2-9=0\\(d-3)(d+3)=0\\\left \{ {{d-3=0 } \atop {d+3=0}} \right. \\\left \{ {{d_{1}=3 } \atop {d_{2}=-3 }} \right.

получится        

\left \{ {{a_{1} =14} \atop {d_{1}=-3 }} \right.

ответ: 14

 

 №3

нечётные числа: 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29

количество нечётных чисел: 12

поиск нечётных чисел по арифметической прогрессии:

от 7 до 29 нечётные числа это 7, 9, ...., 29.

a_{1} =7\\a_{2} =9\\.......\\a_{n} =29

d=a_{n+1}-a_{n}\\d=a_{2}-a_{1} = 9-7=2

a_{n}=a_{1}+(n-1)*d            (a_{n} = 29)

29=7+(n-1)*2\\29=7+2n-2\\29= 2n+5\\2n=29-5\\2n=24\\n=12

получается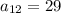 a_{12} = 29

ответ: 12

 №4

S_{7} = ?

a_{3} = 5, d=3

для начала найдём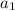 a_{1}, распишем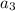 a_{3}

a_{3}=a_{1}+(3-1)*d\\a_{3}=a_{1}+2d\\\\a_{1}=a_{3}-2d\\a_{1}=5-2*3 = -1

воспользуемся формулой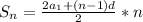 S_{n} =\frac{2a_{1}+(n-1)d }{2}*n

S_{7} =\frac{2a_{1}+(7-1)*3 }{2}*7 = \frac{2*(-1)+6*3}{2} *7 =56

ответ: 56

  №5

a_{1} =4 град. - первый угол

d=110 град

Пусть n углов, тогда сумма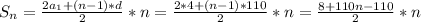  S_{n} =\frac{2a_{1}+(n-1)*d }{2}*n = \frac{2*4+(n-1)*110}{2} *n = \frac{8+110n-110}{2} *n

С другой стороны сумма углов = 180 град*(n-2)

Приравняем и решим уравнение:

\frac{8+110n-110}{2} *n=180n-360    Ι *2

(8+110n-110) *n=360n-720\\8n+110n^2-110n-360n+720=0\\110n^2-462n+720=0

и дальше у меня что-то не выходит......попробуй самим прорешать, может найдёшь у меня ошибку в №5

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
rsharapov rsharapov  11.05.2021 18:10
Постройте G ̅ - дополнение графа G....
КатюшаШамец КатюшаШамец  11.05.2021 18:10
Из 10 м ткани можно сшить одну женскую юбку и 5 детских, а из 20 м этой ткани - 3 такие же женские юбки и 5 детских. Сколько метров ткани необходимо для пошива одной женской юбки...
черныйхащ черныйхащ  11.05.2021 18:09
Задание 1312Сможете решить? ​...
FLASHSAVITAR FLASHSAVITAR  11.05.2021 18:09
2. На соревнованиях по гребле спортсмен 10 мин шел на лодке вниз по течению реки. На обратный путь против течения он затратил 30 мин. Найдите собственную скорость лодки (км/ч),...
yukiko2 yukiko2  11.05.2021 18:09
Сократите: 9×16/8×27; 4×7/28×12; 2×3×5/4×9×25; 7×13-7×2/35×9+35×2.​...
lashina90 lashina90  11.05.2021 18:09
Задуманное мною число равно разности наибольшего двузначного числа с числом 42. Какое число я задумал?. Решение для 2 класса ....
kirmakcim553 kirmakcim553  11.05.2021 18:09
Ребята ! Как решить77053-975310:99990-31357732333333+74368732​...
Минут505 Минут505  11.05.2021 18:08
1. Кратным числа, делитель числа - это 2. Признак делимости на 10 3. Признак делимости на 5 4. Признак делимости на 2 5. Признак делимости на 3 6. Признак делимости на 9 7. Признак...
artemsteam1234oz40fw artemsteam1234oz40fw  11.05.2021 18:08
Знайти точки умовного екстремуму функції z=x/3+y/3 якщо x^2+y^2=1...
dela19 dela19  11.05.2021 18:08
Как решать задачу по учебнику математики 4 часть страница 120 номер 3Б​...

Популярные вопросы