СДАВАТЬ УЖЕ ЧЕРЕЗ ЧАС! Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того,

Question

Математика: СДАВАТЬ УЖЕ ЧЕРЕЗ ЧАС! Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 6.

mashakovalak234 · Answer

Выпишем все числа от 1 до 100, которые содержат цифру 6:

6; 16; 26; 36; 46; 56; 60; 61; 62; 63; 64; 65; 66; 67; 68; 69; 76; 86; 96 - таких чисел 19.

Тогда вероятность вытащить жетон, на котором есть цифра 6, равна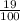 $\frac{19}{100}$ по классическому определению вероятности (вероятность равна отношению благоприятных исходов, которых всего 19, к общему числу исходов, которых всего 100, как и чисел).

Соответственно, вероятность вытащить число, в котором нет цифры 6, равна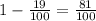 $1-\frac{19}{100}=\frac{81}{100}$

ОТВЕТ: 0,81

Популярные вопросы