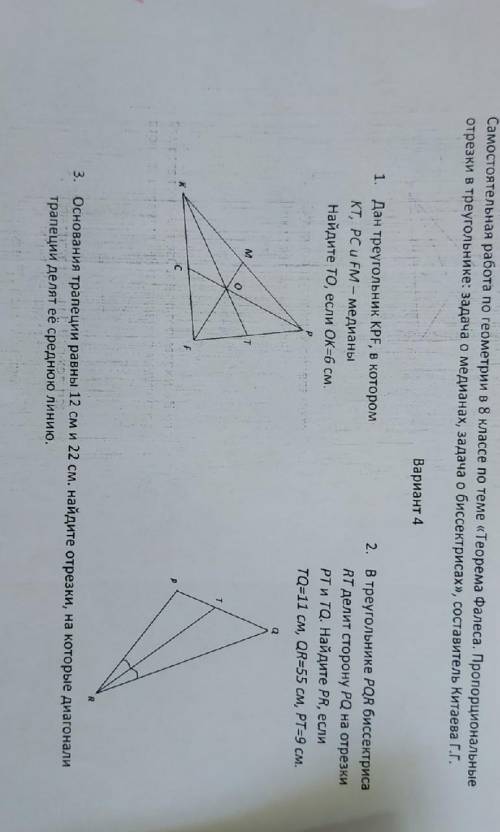
Самостоятельная работа по геометрии 8 классе по теме «Теорема Фалеса. Пропорциональные отрезки в треугольнике задача о медианах, задача о биссектрисах»,​

Добрый день! С радостью помогу вам разобраться с задачей по геометрии на тему "Теорема Фалеса. Пропорциональные отрезки в треугольнике, задача о медианах, задача о биссектрисах".

Данная задача состоит из двух частей. Для начала разберемся с первой частью, связанной с "Теоремой Фалеса" и пропорциональными отрезками.

Нам дан треугольник ABC, внутри которого проведена прямая, пересекающая стороны треугольника в точках D, E и F. Нам нужно доказать, что отрезки, соединяющие соответствующие вершины треугольника с точками пересечения прямой с его сторонами, делятся внутренним и внешним отношением Фалеса.

Для доказательства этого факта воспользуемся понятием подобия треугольников. Вспомним, что два треугольника с одинаковыми углами называются подобными.

На рисунке видно, что треугольники ABC и DEF подобны, так как у них есть два пары соответствующих равных углов: AED и CEF, а также FEB и BDA. Поэтому можно записать пропорцию между сторонами треугольников:

AB/DE = AC/DF = BC/EF

Теперь рассмотрим произвольный точку P на стороне AB. Чтобы доказать равенство внутреннего и внешнего отношения Фалеса, нам нужно показать, что отношение AP/PB равно отношению DE/EF.

Обозначим точку пересечения прямой с стороной BC как M. Построим прямую, параллельную стороне AB и проходящую через точку M. Обозначим точку пересечения этой прямой с стороной AC как N.

Теперь у нас есть два параллельных отрезка: AB и MN. Мы можем использовать теорему о пропорциональности отрезков, которая гласит: если две параллельные прямые пересекают несколько прямых, то отношения соответствующих отрезков на этих пересекаемых прямых равны.

Применим эту теорему к нашей ситуации и подставим известные значения в пропорцию:

AP/PB = AM/MN

Так как прямые AB и MN параллельны, они пересекаются в бесконечности и можно сказать, что длина отрезка NP равна бесконечности. Поэтому получаем:

AP/PB = AM/MN = AM/∞ = AM/0

Теперь обратимся к треугольнику DEF. Поскольку точка P находится на отрезке DE, отрезок DE также делится точкой P на две части: DP и PE.

Запишем пропорцию для отношения длин отрезков DP и PE:

DE/EF = DP/PE

Таким образом, мы получили два равенства:

AP/PB = DP/PE

Левая часть равенства AP/PB соответствует внутреннему отношению Фалеса, а правая часть равенства DP/PE - относительному отношению отрезков в треугольнике DEF.

Таким образом, мы доказали, что отношение AP/PB равно отношению DE/EF, что и требовалось доказать. Внутреннее и внешнее отношение Фалеса верны для данной ситуации.

Перейдем ко второй задаче, связанной с медианами и биссектрисами треугольника. На рисунке видно, что треугольник ABC имеет биссектрису АА1, медиану BD и биссектрису CC1. Нам требуется доказать, что эти three lines пересекаются в одной точке, которая называется центром вписанной окружности треугольника.

Для начала вспомним, что медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Биссектриса - это прямая, проходящая через вершину треугольника и делящая внутренний угол пополам.

Чтобы доказать, что эти три линии пересекаются в одной точке, мы воспользуемся теоремой о сближении треугольников.

Для начала докажем, что биссектриса АА1 делит сторону ВС на отрезки в пропорции сторон треугольника. Обозначим отрезок BC как а, отрезок АС как b и отрезок АВ как c.

Так как АА1 является биссектрисой, она делит сторону ВС на отрезки, пропорциональные смежным сторонам треугольника ABC. Значит:

VC/VS = ВА/АС = c/b

Теперь докажем, что медиана BD делит сторону АС на отрезки в пропорции сторон треугольника ABC.

Так как медиана делит сторону АС пополам, то:

CS/AS = 1/1 = 1

Наконец, докажем, что биссектриса СС1 делит сторону AB на отрезки в пропорции сторон треугольника ABC.

Аналогично предыдущему случаю, так как биссектриса делит сторону AB пополам, то:

АВ/ВС = 1

Получается, что биссектриса АА1 делит сторону ВС в отношении c/b, медиана BD делит сторону АС в отношении 1/1, а биссектриса СС1 делит сторону AB в отношении 1. Заметим, что эти отношения соответствуют отношениям длин заметившихся прям соответственных сторон треугольника ABC.

Теперь обратимся к лемме о сближении треугольников, которая говорит следующее: если три пары изотетических линий треугольника пересекают одну линию, то треугольники соответствующие этим линиям однородны.

В нашей задаче, биссектрисы АА1, СС1 и медиана BD пересекаются в одной точке, следовательно, треугольники соответствующие этим линиям - треугольники AА1СС1 и АВС - однородные.

Так как треугольники однородны, мы можем сказать, что отношения сторон первого треугольника равны соответствующим сторонам треугольника АВС. Из этой равенства следует, что центр окружности вписанной в треугольник АВС должен находиться на пересечении биссектрис АА1, СС1 и медианы BD.

Таким образом, мы доказали, что биссектрисы АА1 и СС1, а также медиана BD пересекаются в одной точке - центре вписанной окружности треугольника ABC.