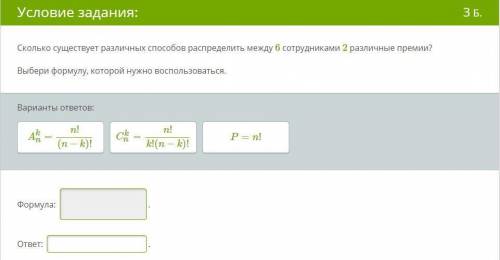
с заданием про вероятность! Сколько существует различных распределить между 6 сотрудниками 2 различные премии? Выбери формулу, которой нужно воспользоваться и решите вероятность.
Другие вопросы по теме Математика
Популярные вопросы
- Найти наименьшие из четырех чисел. нарисуйте блок-схему....
2 - Движение двух мотоциклистов заданы уравнениями x1=12+2t^2 и x2=8t.найти...
1 - Для нагрівання деталі об ємом 0,0007 м3 на 5градус цельсія було витрачено...
3 - 2. вставьте слова в текст и переведите егоcell, lines, microprocessor,...
2 - Сколько грамм сульфата калия можно получить при взаимодействии 31 грамм...
3 - Политическое развитие древней греции...
2 - Сконтрольной, я слишком тупой чтобы это решить...
2 - Формулы привидения для аргумента 2π-a...
2 - Тысячи путей ведут к заблуждению ,к истине - только один. сколько объём...
3 - Написать молекулу 4,4-дибропентен-1...
2
Формула размещений дает нам количество способов выбрать k элементов из n, учитывая их порядок. В данной задаче нам нужно выбрать 2 сотрудников из 6, чтобы наградить их премиями. При этом сотрудники являются различными, то есть мы должны учесть их различие при распределении премий. Поэтому мы будем использовать формулу размещений.
Формула размещений:
A(n, k) = n! / (n-k)!
Где n - общее количество элементов (сотрудников), k - количество элементов, которые мы выбираем (премии), ! - знак факториала.
Подставим значения в формулу и рассчитаем количество способов:
A(6, 2) = 6! / (6-2)!
= 6! / 4!
= (6 * 5 * 4!) / 4!
= (6 * 5) / 1
= 30
Таким образом, существует 30 различных способов распределить 2 различные премии между 6 сотрудниками.
Теперь, чтобы найти вероятность, нужно разделить количество успешных исходов на общее количество возможных исходов. В данном случае количество успешных исходов равно 30, а общее количество возможных исходов - это общее количество способов распределить премии, а именно 30.
Таким образом, вероятность равна:
P = количество успешных исходов / общее количество возможных исходов
= 30 / 30
= 1
Итак, вероятность составляет 1 или 100%. Это означает, что в данном случае распределение премий с 100% вероятностью будет успешным.