с заданием по высшей математике Задание 9,10
Чертить кривые не нужно
Дана кривая x^2 + 4y = 0. Докажите, что данная кривая — парабола. Найдите координаты её вершины. Найдите значение её параметра p. Запишите уравнение её оси симметрии.
Дана кривая 5x^2 + 8y^2 + 4xy − 24x − 24y = 0. Докажите, что эта кривая — эллипс. Найдите координаты центра его симметрии. Найдите его большую и малую полуоси. Запишите уравнение фокальной оси.
Другие вопросы по теме Математика
Популярные вопросы
- 50бл. Проаналізуйте поезію за такою схемою (тема, ідея; жанрові...
1 - Дополнительные задания для 1. ВВыпуклом многоугольнике число...
1 - 10. Complete the second sentence so that it means the same as...
1 - Что такое обрядые и необрядовые? по музыке...
2 - сделать 4 и к нему нижнее задание...
2 - Задание 3. Приведите примеры дипломатических отношений Византийской...
2 - . Прочитайте статтю «Вільшаний король» Ґете в музиці. Послухайте...
2 - 1-мәтін 2-мәтін Құжаттардың ататулары (жанрлары) Құжаттар қандай...
2 - нужно сделать выписать причастный и деепричастный оборот выделить...
1 - Морфологический разбор приходиться из туч...
3
9.2. (0, 0)
9.3. p = 2
9.4. x = 0
10.2. (2, 1)
10.3. a = 2, b = 3
10.4. x + 2y - 4 = 0
Пояснение:
9.1. Каноническое уравнение параболы можно записать в виде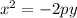 . В нашем случае
. В нашем случае 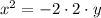 , что соответствует этому уравнению.
, что соответствует этому уравнению.
9.2. Поскольку уравнение соответствует каноническому, преобразования координат не произошло. Значит, вершина параболы находится в точке (0, 0).
9.3. Из п. 9.1 p = 2.
9.4. Если точка (x, y) принадлежит параболе, то и точка (-x, y) принадлежит ей (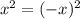 ), значит, её ось симметрии — прямая x = 0.
), значит, её ось симметрии — прямая x = 0.
10.1. Выполним поворот на угол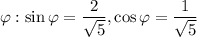 . Воспользуемся формулами
. Воспользуемся формулами 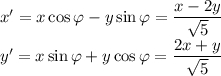 :
:
Выполним параллельный перенос начала координат на вектор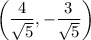 . Воспользуемся формулами
. Воспользуемся формулами 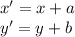 (a, b — координаты вектора):
(a, b — координаты вектора):
Поделим обе части уравнения на 36:
Получили каноническое уравнение эллипса.
10.2. В полученном в п. 10.1 уравнении центр симметрии находится в точке (0, 0). Чтобы получить центр симметрии исходного эллипса, необходимо провести преобразования координат в обратном порядке (поскольку действия проводились над системой координат, а теперь — над точкой, то формулы останутся такими же):
параллельный перенос:10.3. Из уравнения, полученного в п. 10.1: большая полуось b = 3, малая полуось a = 2.
10.4. Уравнение фокальной оси в полученном уравнении: x = 0. Выполним преобразования координат в обратном порядке:
параллельный перенос: