с тригонометрическим уравнением
Другие вопросы по теме Математика
Популярные вопросы
- Зробіть будь-ласка підписи зовнішньої бруньки...
1 - Число n кратне 4. Чому може дорівнювати остача при діленні числа m...
3 - Вариант решить , нужно решить все задания , полугодовая консольная...
1 - Сколько атомов углерода содержит углеродная цепь соединений: 1.метаналь;...
3 - напишите 5 речень чем мне не нравится история....
2 - Найти относительную погрешность следующих измерений: радиуса Земли:...
1 - 12/x+6=x-4/8 Чему равен x?...
3 - Прокомментируйте предложенную оценку личности последнего российского...
1 - Число b при діленні на 5 дає в остачі 2, а при діленні на 3 дає в остачі...
1 - Чим небезпечний атеросклероз? Як запобігти цій хворобі?...
2
Для удобства: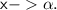
Подстановка:
При k=-1:
Делаем вывод, что наибольший отрицательный корень: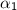
Значит,
2 вариант ответа.