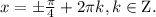с тригонометрическим уравнением
Другие вопросы по теме Математика
Популярные вопросы
- Найдите периметр прямоугольника площадь которого 5м2 и одна из сторон 2/5м...
2 - Если в четверти выходит 3.54 сколько надо пятёрок чтоб было 3.80 а сколько...
3 - Согласно пакту молотова - риббентропа, и германия договорилась о: а) аншлюсе...
1 - Друг она моя душа пошатнулась не дыша как эти слова отношение пушкина к царевне...
2 - 1. сложность 1. из школы домой. даша и петя живут в одном доме и в одном...
3 - Вставить слова в предложениях my school for the new year...
1 - Народы, населяющие страну замбию. и их основные занятия....
3 - Ялюблю музыку. я люблю классическую музыку. композиторы которых я знаю (пр....
3 - Сполучне слово в складнопідрядному реченні хлопці збирали по дорозі повні...
1 - Как решить периметр прямоугольника равен 54 сантиметров основания на 5 сантиметров...
1
5)
Пошаговое объяснение:
Если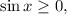 получаем уравнение
получаем уравнение
при этом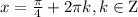 удовлетворяют условию
удовлетворяют условию 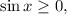 а
а 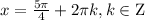 — не удовлетворяют.
— не удовлетворяют.
Если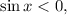 аналогично:
аналогично:
Из найденных корней только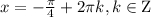 удовлетворяет условию
удовлетворяет условию 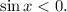
Таким образом, решения нашего уравнения