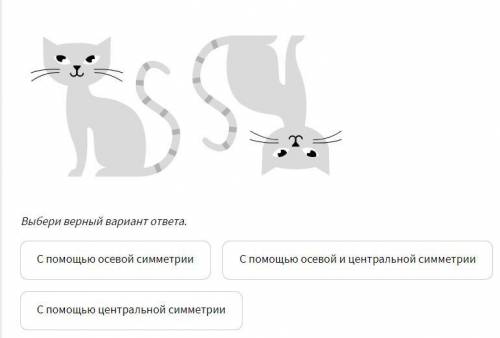
С симметрии какого типа можно получить такое расположение фигур?

С помощью осивой симметрий

На изображении мы видим расположение двух фигур: синего треугольника и красного прямоугольника. Чтобы определить, с какой симметрией можно получить такое расположение фигур, нужно рассмотреть особенности этого расположения.

1. Прямая симметрия (ось симметрии):
Рассмотрим синий треугольник. Если мы проведем вертикальную прямую, проходящую через вершину треугольника (с названием A), то мы увидим, что все точки, противоположные к названию, лежат на этой прямой. То же самое можно сказать и о другой вершине, названной B. Таким образом, форма треугольника сохраняется, если его отразить вдоль этой вертикальной прямой.

Однако, если мы проведем горизонтальную прямую, проходящую через треугольник, то не все точки будут противоположными друг другу. Поэтому, прямоугольника нет оси симметрии. Следовательно, данное расположение фигур не может быть получено с помощью прямой симметрии.

2. Осевая симметрия:
Рассмотрим красный прямоугольник. Если мы проведем вертикальную прямую, проходящую через середину левого и правого ребра прямоугольника, то мы увидим, что фигура делится на две зеркально-симметричные части. Отображение одной части по отношению к другой может совпасть с данным расположением фигур.

Теперь рассмотрим синий треугольник. Как уже упоминалось, он имеет ось симметрии, но эта ось не пересекается с прямым проложением прямоугольника. Следовательно, осевая симметрия не может дать такое расположение фигур.

3. Групповая симметрия (также известная как повороты):
Ответ на этот вопрос может быть получен с использованием групповой симметрии. Если мы представим, что треугольник центрирован на точке, проходящей через его вершины (противоположные стороны треугольника совпадают), то мы можем повернуть его на определенный угол в направлении против часовой стрелки для создания такого расположения, где вершина треугольника соответствует верхнему ребру прямоугольника и две другие вершины треугольника лежат симметрично относительно вертикальной оси прямоугольника.

Таким образом, данное расположение фигур может быть получено с помощью групповой симметрии, осуществляя поворот треугольника на нужный угол относительно его центра.