1. Математика
  2. с решением корень из x+3 -

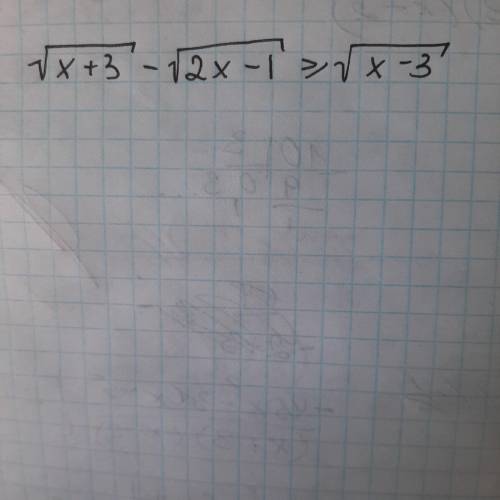
с решением корень из x+3 - корень из 2x-1 ⩾ корень из x-3


с решением корень из x+3 - корень из 2x-1 ⩾ корень из x-3

Arseniy2828 Arseniy2828    2   10.07.2021 19:32    0

Ответы
sofija97 sofija97  09.08.2021 20:30

(см. объяснение)

Пошаговое объяснение:

\sqrt{x+3}-\sqrt{2x-1}\ge\sqrt{x-3}\\\sqrt{x+3}\ge\sqrt{x-3}+\sqrt{2x-1}\\x+3\ge x-3+2\sqrt{(x-3)(2x-1)}+2x-1\\7-2x\ge2\sqrt{(x-3)(2x-1)

Сделаем равносильный переход на условии, что x\in\left(-\infty;\;\dfrac{1}{2}\right]\cup\left[3;\;\dfrac{7}{2}\right]:

49-28x+4x^2\ge4(2x^2-7x+3)\\4x^2-37\le0\\x^2\le\dfrac{37}{4}\\x\in\left[-\dfrac{\sqrt{37}}{2};\;\dfrac{\sqrt{37}}{2}\right]

Тогда ответом будет:

x\in\left[3;\;\dfrac{\sqrt{37}}{2}\right]

Неравенство решено!

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
sokolovsokol3андрей sokolovsokol3андрей  18.05.2019 05:50
Вдвух корзинах лежало 84 яблока. когда из одной корзины переложили во вторую 15 яблок, то во второй корзине яблок оказалось в 3 раза больше, чем в первой. сколько яблок было в каждой...
10672 10672  18.05.2019 05:50
1)ширину прямоугольника уменьшили на 30%, а длину увеличили на одну треть. уменьшилась или увеличилась площадь прямоугольника, и на сколько процентов? 2)разность двух чисел равна...
algebraigeometria1 algebraigeometria1  18.05.2019 05:50
1) на стройку доставили на 24 грузовиках песок, по 4т 50ц на каждом, а на 35 грузовиках щебень, по 2т 75ц на каждом. сколько всего песка и щебня доставили эти грузовики на стройку?...
Anna13701 Anna13701  18.05.2019 05:50
3/8 - 0,375+х выражение м+5/9-2/3только быстро ,1 лучшее решение...
Dewerro Dewerro  18.05.2019 05:50
До конца суток осталось вдвое меньше времени от их начала который час ?...
kuznechikmarin kuznechikmarin  18.05.2019 05:50
Решите уравнение неизвестное число плюс 240 умножить на 3 равно 1260...
vitakotov009 vitakotov009  18.05.2019 05:50
М. в богданович 4 класс №772 страница 116 в овощехранилище было 39т 600кг картофеля. в первый день из овощехранилища вывезли 9100 этого количества, во втрой день 19 остатка. сколько...
Юриякамория Юриякамория  18.05.2019 05:50
А)одно число больше другого на 56. сумма этих чисел равна 420.найдите числа б) одно число меньше другого на 105. сумма этих чисел равна 203.найдите числа...
koshulinskayag koshulinskayag  18.05.2019 05:50
Коля и юра одновременно вышли из школы в противоположных направлениях. коля м, а юра - в 3 раза больше. на каком расстоянии друг от друга находятся мальчики? на сколько меньше метров...
igor99kz igor99kz  18.05.2019 05:50
Сравните дроби: 15,38 и 15,4; 3,250 и 3,25...

Популярные вопросы