с примером. ответ должен получиться: 8
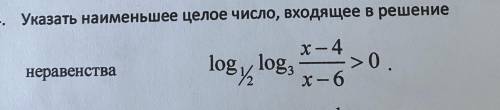
Другие вопросы по теме Математика
Популярные вопросы
- Олена комова.твір мій сусід-прибулець.придумати припущення.4...
1 - Погомогит зайдите в коментариипростите что так мало даюподписывайтесь...
3 - Разложите множители 9x^2-6xyA^3+3a^2+3a+9X^3-8y^3ПОСТАВЛИ ЛУТШИЙ...
1 - Распределить старославянизмы по тематическим группам. Наименования...
3 - Какие образованич слов вам известны?...
3 - 2 Put the verbs into Past Simple or Past Continuous. We (1. pack)...
3 - Дано: -5→а→-3. Оцінити значення виразу 1/a....
2 - на кого распространяется административная, военная, духовная,...
1 - Питання до «Червоне і чорне» Хелпп 1. Про що мріяв Жульєн Сорель?...
3 - Разложить на множители:1/8а²-а⁵...
1
Заметим, что основание логарифма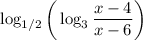 меньше единицы. Это означает, чтобы значение самого логарифма было больше ноля (как требуется в неравенстве), нужно, чтобы его подлогарифмическое выражение было тоже меньше единицы (и больше ноля, в силу области определения логарифмических выражений):
меньше единицы. Это означает, чтобы значение самого логарифма было больше ноля (как требуется в неравенстве), нужно, чтобы его подлогарифмическое выражение было тоже меньше единицы (и больше ноля, в силу области определения логарифмических выражений):
Все это можно довести до метода интервалов:
Первое неравенство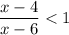 можно решить так:
можно решить так:
- - - + + +
__________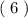 __________
__________ 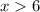
Второе неравенство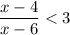 решается схожим образом:
решается схожим образом:
- - - + + + - - -
_________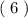 _________
_________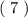 _________ Или
_________ Или 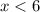 , или
, или 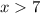 .
.
Как пересечение решений двух неравенств имеем решение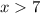 .
.
Значит, наименьшее целое число, удовлетворяющее неравенству - это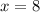 , что сходится с ответом.
, что сходится с ответом.
ответ: 8.