с пояснением
"найти наибольшее и наименьшие значение функции на отрезке "
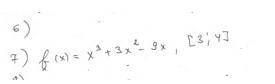
Другие вопросы по теме Математика
Популярные вопросы
- Написать письмо на завтро надо you have got a letter from your english-speaking...
1 - Разберите по членам предложения.утомленная зноем странница с наслаждением пила воду...
1 - Решить : c клавиатуры вводится число n . если оно положительное ,то выведите n^2(n*n).а...
2 - Составьте предложение кроме отважного солдата помимо уроков...
1 - Look at pictures and answer the question: what did santa claus yesterday?...
2 - Как вы понимаете утверждение относись к другим так, как ты хотел, чтобы относились...
3 - Обоснуйте какое из чисел больше или...
2 - Продолжи тезис дружба- аргумента и заключение...
2 - Каковы были основные причины восстаний середины 19 века семиречье и южного казахстана...
2 - Как ведет себя главный герой в разных ситуациях в повести приключения тома сойера?...
2
f наиб = 76; f наим = 27
Пошаговое объяснение:
Функция
f(x) = x³ + 3x² - 9x
Производная функции
f'(x) = 3x² + 6x - 9
Найдём точки экстремумов
3x² + 6x - 9 = 0
x² + 2x - 3 = 0
D = 4 + 12 = 16 = 4²
x₁ = 0.5 (-2 - 4) = -3 - точка максимума
х₂ = 0,5(-2 + 4) = 1 - точка минимума
При х ≥ 1 функция возрастает, поэтому в интервале х ∈ [3; 4] функция имеет наименьшее значение при х = 3, а наибольшее значение - при х = 4.
f наиб = f(4) = 4³ + 3 · 4² - 9 · 4 = 64 + 48 - 36 = 76
f наим = f(3) = 3³ + 3 · 3² - 9 · 3 = 27 + 27 - 27 = 27